题目内容
16.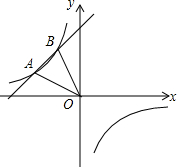 如图,一次函数的图象与反比例函数y=$\frac{m}{x}$的图象交于A(-4,a)、B两点,点B的横坐标比点A的横坐标大2,且S△AOB=6.
如图,一次函数的图象与反比例函数y=$\frac{m}{x}$的图象交于A(-4,a)、B两点,点B的横坐标比点A的横坐标大2,且S△AOB=6.(1)求m的值;
(2)求直线AB的解析式;
(3)指出一次函数值大于反比例函数值时x的取值范围.
分析 (1)过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,根据反比例函数相似k的几何意义得出S梯形ACDB=S△AOB=6,根据梯形的面积得出关于m的方程,解方程即可;
(2)先求得A、B的坐标,然后根据待定系数法即可求得;
(3)根据图象即可求得.
解答 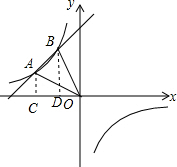 解:(1)过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,则S梯形ACDB=S△AOB=6,
解:(1)过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,则S梯形ACDB=S△AOB=6,
∴$\frac{1}{2}$(AC+BD)•CD=6,
∴-$\frac{m}{4}$-$\frac{m}{2}$=6,
∴m=-8.
(2)∵一次函数的图象与反比例函数y=-$\frac{8}{x}$的图象交于A(-4,a)、B两点,点B的横坐标比点A的横坐标大2,
∴a=-$\frac{8}{-4}$=2,
∴A(-4,2),B(-2,4),
设直线AB的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{-4k+b=2}\\{-2k+b=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1}\\{b=6}\end{array}\right.$,
∴直线AB的解析式为y=x+6.
(3)一次函数值大于反比例函数值时x的取值范围是-4<x<-2或x>0.
点评 本题考查了反比例函数和一次函数的交点问题,反比例函数系数k的几何意义,待定系数法求一次函数的解析式,以及函数与不等式的关系等,关键是做出辅助线,构造梯形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.下列命题错误的是( )
| A. | 平行四边形的对角线互相平分 | |
| B. | 对角线互相垂直平分的四边形是菱形 | |
| C. | 矩形的对角线相等 | |
| D. | 对角线相等的四边形是正方形 |
7. 如图,直线a∥b,直角三角板ABC的直角顶点C在直线b上,∠1=35°,则∠2的度数是( )
如图,直线a∥b,直角三角板ABC的直角顶点C在直线b上,∠1=35°,则∠2的度数是( )
 如图,直线a∥b,直角三角板ABC的直角顶点C在直线b上,∠1=35°,则∠2的度数是( )
如图,直线a∥b,直角三角板ABC的直角顶点C在直线b上,∠1=35°,则∠2的度数是( )| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
4. 如图,矩形ABCD和矩形CEFG中,AD=2,AB=1,CE=3,EF=6,连接AF,H是AF的中点,那么CH的长是( )
如图,矩形ABCD和矩形CEFG中,AD=2,AB=1,CE=3,EF=6,连接AF,H是AF的中点,那么CH的长是( )
 如图,矩形ABCD和矩形CEFG中,AD=2,AB=1,CE=3,EF=6,连接AF,H是AF的中点,那么CH的长是( )
如图,矩形ABCD和矩形CEFG中,AD=2,AB=1,CE=3,EF=6,连接AF,H是AF的中点,那么CH的长是( )| A. | $\frac{5}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{5}{2}$$\sqrt{2}$ | D. | 2 |

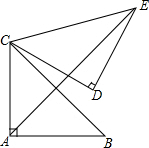 如图,在△ABC中,∠BAC=90°,AB=AC=2,将△CAB绕着点C逆时针旋转60°,得到△CDE,连接AE,则AE的长是$\sqrt{2}$+$\sqrt{6}$.
如图,在△ABC中,∠BAC=90°,AB=AC=2,将△CAB绕着点C逆时针旋转60°,得到△CDE,连接AE,则AE的长是$\sqrt{2}$+$\sqrt{6}$. 如图,已知菱形ABCD的周长20,sin∠ABD=$\frac{3}{5}$,求菱形ABCD的面积.
如图,已知菱形ABCD的周长20,sin∠ABD=$\frac{3}{5}$,求菱形ABCD的面积.