题目内容
9．
已知反比例函数y=$\frac{k}{x}$的图象如图所示，则二次函数y=-kx2-2x+$\frac{{k}^{2}}{4}$的图象大致为（ ）| A． |  | B． |  | C． |  | D． |  |
分析 由点（1，2）在反比例函数图象上，利用待定系数法即可求出k值，将其代入二次函数解析式中，结合二次项系数a和抛物线的对称轴x=-$\frac{b}{2a}$，即可得出结论．
解答 解：∵点（1，2）在反比例函数图象上，
∴有2=$\frac{k}{1}$，解得：k=2．
∴二次函数解析式为y=-2x2-2x+1．
∵a=-2＜0，
∴抛物线开口向下；
∵-$\frac{b}{2a}$=-$\frac{-2}{2×（-2）}$=-$\frac{1}{2}$，
∴抛物线的对称轴为x=-$\frac{1}{2}$．
故选B．
点评 本题考查了待定系数法求反比例函数解析式以及二次函数的图象，解题的关键是利用待定系数法求出k值．本题属于基础题，难度不大，解决该题型题目时，由点的坐标利用待定系数法求出k的值是关键．
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目
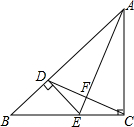已知，如图，△ABC中，AC=BC，∠C=90°，AE平分∠BAC交BC于E，过E做ED⊥AB于D，连接DC交AE于F，其中BD=1．则在下列结论中：①AE⊥DC；②AB=2+$\sqrt{2}$；③$\frac{AE}{CD}$=2；④AE•CD=2+2$\sqrt{2}$．其中正确的结论是①②④．
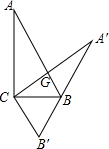如图，在Rt△ABC中，∠C=90°，BC=5，tanB=2，把△ABC绕点C旋转得到△A′B′C，此时AB的对应边A′B′恰好经过点B，又A′C交AB于点G，则线段CG的长是$\frac{50}{11}$．
17．2015年8月18日，第三届中国绿色博览会在天津开吗，坐落在“新时代”板块的天津园面积最大，达11000平方米，将11000用科学记数法表示应为（ ）
| A． | 0.11×105 | B． | 1.1×104 | C． | 11×103 | D． | 11×104 |
4．
如图，矩形ABCD和矩形CEFG中，AD=2，AB=1，CE=3，EF=6，连接AF，H是AF的中点，那么CH的长是（ ）
如图，矩形ABCD和矩形CEFG中，AD=2，AB=1，CE=3，EF=6，连接AF，H是AF的中点，那么CH的长是（ ）| A． | $\frac{5}{2}$ | B． | $\sqrt{5}$ | C． | $\frac{5}{2}$$\sqrt{2}$ | D． | 2 |
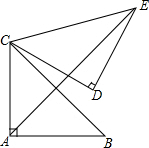如图，在△ABC中，∠BAC=90°，AB=AC=2，将△CAB绕着点C逆时针旋转60°，得到△CDE，连接AE，则AE的长是$\sqrt{2}$+$\sqrt{6}$．
18．计算：$\frac{{a}^{2}-1}{{a}^{2}+2a+1}$÷$\frac{a-1}{a}$，其结果正确的是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{a}{a+1}$ | C． | $\frac{a+1}{a}$ | D． | $\frac{a+1}{a+2}$ |