题目内容
14. 如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=$\frac{k}{x}$(x>0)经过斜边OA的中点C,与另一直角边交于点D,若S△OCD=6,则S△OBD的值为4.
如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=$\frac{k}{x}$(x>0)经过斜边OA的中点C,与另一直角边交于点D,若S△OCD=6,则S△OBD的值为4.
分析 过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值,即S=$\frac{1}{2}$|k|.
解答 解:如图,过C点作CE⊥x轴,垂足为E.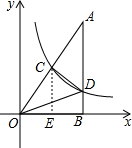
∵Rt△OAB中,∠OBA=90°,
∴CE∥AB,
∵C为Rt△OAB斜边OA的中点C,
∴CE为Rt△OAB的中位线,
∵△OEC∽△OBA,
∴$\frac{OC}{OA}$=$\frac{1}{2}$.
∵双曲线的解析式是y=$\frac{k}{x}$,即xy=k
∴S△BOD=S△COE=$\frac{1}{2}$|k|,
∴S△AOB=4S△COE=2|k|,
由S△AOB-S△BOD=S△AOD=2S△DOC=12,得2k-$\frac{1}{2}$k=12,
k=8,
S△BOD=S△COE=$\frac{1}{2}$k=4.
故答案是:4.
点评 本题考查了反比函数k的几何意义,过图象上的任意一点作x轴、y轴的垂线,所得三角形的面积是$\frac{1}{2}$|k|,是经常考查的知识点,也体现了数形结合的思想.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
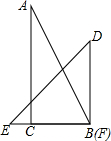 一副直角三角板按如图所示摆放一起,使等腰三角板DEF的直角顶点F与另一块直角三角板ABC的锐角顶点B(∠B=60°)重合,直角边BC与EF重合,此时两块直角三角板的斜边AB与DE的夹角(夹角指锐角或直角)是75°.
一副直角三角板按如图所示摆放一起,使等腰三角板DEF的直角顶点F与另一块直角三角板ABC的锐角顶点B(∠B=60°)重合,直角边BC与EF重合,此时两块直角三角板的斜边AB与DE的夹角(夹角指锐角或直角)是75°. 如图,在Rt△ABC中,AC=5,BC=12,将Rt△ABC沿AD折叠后,使点C落在AB上的点E处,求CD.
如图,在Rt△ABC中,AC=5,BC=12,将Rt△ABC沿AD折叠后,使点C落在AB上的点E处,求CD. 如图,在△ABC中,∠A=60°,BC=10,BO平分∠ABC,CO平分∠ACB,MN经过点O与AB,AC相交于点M,N,且MN∥BC,△AMN的周长为18.
如图,在△ABC中,∠A=60°,BC=10,BO平分∠ABC,CO平分∠ACB,MN经过点O与AB,AC相交于点M,N,且MN∥BC,△AMN的周长为18.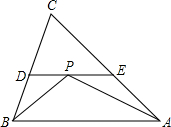 如图,△ABC中,∠ABC,∠CAB的平分线交于点P,过点P作DE∥AB,分别交BC,AC于点D,E.
如图,△ABC中,∠ABC,∠CAB的平分线交于点P,过点P作DE∥AB,分别交BC,AC于点D,E.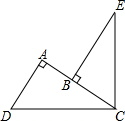 如图,∠DCE=90°,∠DAC=90°,BE⊥AC于点B,且DC=EC,请证明:AB+AD=BE.
如图,∠DCE=90°,∠DAC=90°,BE⊥AC于点B,且DC=EC,请证明:AB+AD=BE.