题目内容
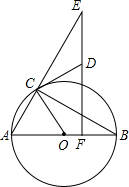 如图,AB为⊙O的直径,∠ABC=30°,ED⊥AB于点F,CD切⊙O于点C,交EF于点D.
如图,AB为⊙O的直径,∠ABC=30°,ED⊥AB于点F,CD切⊙O于点C,交EF于点D.(1)∠E=
(2)△DCE是什么特殊三角形?请说明理由;
(3)当⊙O的半径为1,BF=
3-
| ||
| 2 |
考点:切线的性质,全等三角形的判定,勾股定理
专题:
分析:(1)ED⊥AB于点F,∠EFA=90°所以∠E+∠A=90°.AB为⊙O的直径,∠ACB=90°所以∠A+∠ABC=90°,∠E=∠ABC=30°;
(2)CD是⊙O的切线,得∠OCD=90°即∠1+∠3=90°,∠ECB=90°,即∠2+∠3=90°,∠1=∠2.于是得∠2=∠E=30°,DE=CD,进而可知此三角形为等腰三角形;
(3)由勾股定理求得BC=
,然后由直角三角形的性质,求得CE=
,即可证得△DCE≌△OCB.
(2)CD是⊙O的切线,得∠OCD=90°即∠1+∠3=90°,∠ECB=90°,即∠2+∠3=90°,∠1=∠2.于是得∠2=∠E=30°,DE=CD,进而可知此三角形为等腰三角形;
(3)由勾股定理求得BC=
| 3 |
| 3 |
解答:(1)解:∵ED⊥AB于点F,
∴∠EFA=90°.
∴∠E+∠A=90°.
∵AB为⊙O的直径,
∴∠ACB=90°
∴∠A+∠ABC=90°
∴∠E=∠ABC=30°;
(2)解:△DCE为等腰三角形.理由如下:
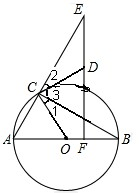 ∵CD是⊙O的切线,
∵CD是⊙O的切线,
∴∠OCD=90°.
即∠1+∠3=90°.
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠ECB=90°,即∠2+∠3=90°,
∴∠1=∠2.
∵∠B=30°,
∴∠A=60°;
∵OC=OB,
∴∠1=∠B=30°,
∴∠2=30°.
∵∠E=30°,
∴∠E=∠2,
∴DE=CD.
故△DCE的等腰三角形;
(3)证明:在Rt△ABC中,∵∠B=30°,
∴AC=
AB=
×2=1.
∴BC=
=
.
AF=AB-BF=2-
=
,
在Rt△AEF中,∵∠E=30°,
∴AE=2AF=1+
,
∴CE=AE-AC=1+
-1=
.
在△DCE和△OCB中,
∵∠E=∠2=∠B=∠1=30°,CE=BC=
,
∴在△DCE和△OCB中,
∴△DCE≌△OCB.
∴∠EFA=90°.
∴∠E+∠A=90°.
∵AB为⊙O的直径,
∴∠ACB=90°
∴∠A+∠ABC=90°
∴∠E=∠ABC=30°;
(2)解:△DCE为等腰三角形.理由如下:
 ∵CD是⊙O的切线,
∵CD是⊙O的切线,∴∠OCD=90°.
即∠1+∠3=90°.
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠ECB=90°,即∠2+∠3=90°,
∴∠1=∠2.
∵∠B=30°,
∴∠A=60°;
∵OC=OB,
∴∠1=∠B=30°,
∴∠2=30°.
∵∠E=30°,
∴∠E=∠2,
∴DE=CD.
故△DCE的等腰三角形;
(3)证明:在Rt△ABC中,∵∠B=30°,
∴AC=
| 1 |
| 2 |
| 1 |
| 2 |
∴BC=
| AB2-AC2 |
| 3 |
AF=AB-BF=2-
3-
| ||
| 2 |
1+
| ||
| 2 |
在Rt△AEF中,∵∠E=30°,
∴AE=2AF=1+
| 3 |
∴CE=AE-AC=1+
| 3 |
| 3 |
在△DCE和△OCB中,
∵∠E=∠2=∠B=∠1=30°,CE=BC=
| 3 |
∴在△DCE和△OCB中,
|
∴△DCE≌△OCB.
点评:本题主要考查了切线的性质、圆周角定理的推论、等腰三角形的判定、直角三角形的性质以及全等三角形的判定,综合性较强.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
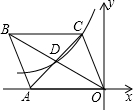 如图,?OABC中顶点A在x轴负半轴上,B、C在第二象限,对角线交于点D,若C、D两点在反比例函
如图,?OABC中顶点A在x轴负半轴上,B、C在第二象限,对角线交于点D,若C、D两点在反比例函 已知:如图,AB是半圆O的直径,CD⊥AB于D点,AD=4cm,DB=8cm,求BC的长.
已知:如图,AB是半圆O的直径,CD⊥AB于D点,AD=4cm,DB=8cm,求BC的长.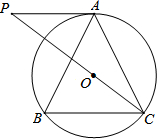 如图,⊙O是△ABC的外接圆,AB=AC,连结CO并延长交⊙O的切线AP于点P.
如图,⊙O是△ABC的外接圆,AB=AC,连结CO并延长交⊙O的切线AP于点P.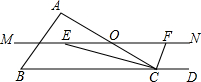 如图,在△ABC中,点O是AC边上的一点.过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于F.
如图,在△ABC中,点O是AC边上的一点.过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于F.