题目内容
已知：如图，AB是半圆O的直径，CD⊥AB于D点，AD=4cm，DB=8cm，求BC的长．考点：相似三角形的判定与性质,圆周角定理
专题：
分析：连接AC，由△ADC∽△BDC，可以得到答案．
解答：
解：连接AC，因为AB是⊙O的直径，
所以∠ACB=90°，CD⊥AB，
所以∠ADC=90°，
所以△ACD∽△BCD，
所以CD2=AD•BD，
又因为AD=4cm，BD=8cm，
所以CD=4
cm，
根据勾股定理得：BC=4
cm．
所以BC的长度为4
cm．
解：连接AC，因为AB是⊙O的直径，所以∠ACB=90°，CD⊥AB，
所以∠ADC=90°，
所以△ACD∽△BCD，
所以CD2=AD•BD，
又因为AD=4cm，BD=8cm，
所以CD=4
| 2 |
根据勾股定理得：BC=4
| 6 |
所以BC的长度为4
| 6 |
点评：本题考查了三角形相似的判定，以及利用勾股定理求线段的长度．
练习册系列答案
同步奥数系列答案
相关题目
如图，在平行四边形ABCD中，下列结论中错误的是（ ）| A、∠1=∠2 |
| B、∠BAD=∠BCD |
| C、AB=CD |
| D、AC=BC |
对于一组统计数据：2，3，5，6，4，4，下列说法错误的是（ ）
| A、众数是4 | B、中位数是4 |
| C、平均数是4 | D、方差是4 |
关于x的分式方程
=1，下列说法正确的是（ ）
| a |
| x+3 |
| A、方程的解是x=a-3 |
| B、当a＞3时，方程的解是正数 |
| C、当a＜3时，方程的解为负数 |
| D、以上答案都正确 |
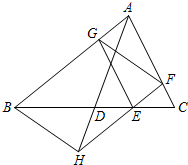已知：如图，在△ABC中，AD是边BC上的中线，点E在线段DC上，EF∥AB交边AC于点F，EG∥AC交边AB于点G，FE的延长线与AD的延长线交于点H．
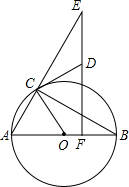如图，AB为⊙O的直径，∠ABC=30°，ED⊥AB于点F，CD切⊙O于点C，交EF于点D．
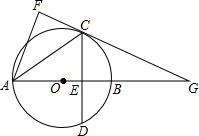如图，在⊙O中，直径AB垂直于弦CD，垂足为E，连AC，将△ACE沿AC翻折得到△ACF，直线CF与直线AB相交于G．
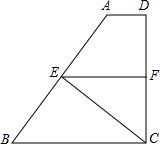梯形ABCD中，AD∥BC，DC⊥BC，CE⊥AB于点E，点F在边CD上，且BE•CE=BC•CF．