题目内容
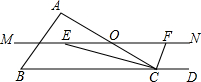 如图,在△ABC中,点O是AC边上的一点.过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于F.
如图,在△ABC中,点O是AC边上的一点.过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于F.(1)求证:EO=FO;
(2)若CE=4,CF=3,你还能得到那些结论?
考点:等腰三角形的判定与性质,勾股定理
专题:
分析:(1)根据角平分线的定义可得∠1=∠2,根据两直线平行,内错角相等可得∠1=∠3,然后求出∠2=∠3,再根据等角对等边可得OE=OC,同理可得OF=OC,从而得到OE=OF;
(2)CE是∠ACB的平分线,CF是∠OCD的平分线,所以∠ECF=90°,若CE=4,CF=3,得到EF=5,OE=OF=OC=
.
(2)CE是∠ACB的平分线,CF是∠OCD的平分线,所以∠ECF=90°,若CE=4,CF=3,得到EF=5,OE=OF=OC=
| 5 |
| 2 |
解答:解:(1)∵CE是∠ACB的平分线,
∴∠1=∠2,
∵MN∥BC,
∴∠1=∠3,
∴∠2=∠3,
∴OE=OC,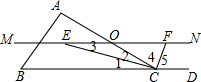
同理可得OF=OC,
∴OE=OF;
(2)∵CE是∠ACB的平分线,
∴∠1=∠2,
∵CF是∠OCD的平分线,
∴∠4=∠5,
∴∠ECF=90°,
在Rt△ECF中,由勾股定理得
EF=
=
=5.
∴OE=OF=OC=
EF=
.
∴∠1=∠2,
∵MN∥BC,
∴∠1=∠3,
∴∠2=∠3,
∴OE=OC,

同理可得OF=OC,
∴OE=OF;
(2)∵CE是∠ACB的平分线,
∴∠1=∠2,
∵CF是∠OCD的平分线,
∴∠4=∠5,
∴∠ECF=90°,
在Rt△ECF中,由勾股定理得
EF=
| CE2+CF2 |
| 42+32 |
∴OE=OF=OC=
| 1 |
| 2 |
| 5 |
| 2 |
点评:本题考查了等腰三角形的判定与性质,角平分线的定义,平行线的性质,熟记性质是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若一个数的相反数是2,则这个数是( )
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
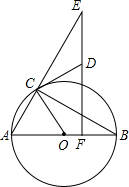 如图,AB为⊙O的直径,∠ABC=30°,ED⊥AB于点F,CD切⊙O于点C,交EF于点D.
如图,AB为⊙O的直径,∠ABC=30°,ED⊥AB于点F,CD切⊙O于点C,交EF于点D.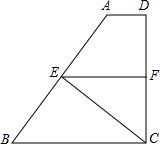 梯形ABCD中,AD∥BC,DC⊥BC,CE⊥AB于点E,点F在边CD上,且BE•CE=BC•CF.
梯形ABCD中,AD∥BC,DC⊥BC,CE⊥AB于点E,点F在边CD上,且BE•CE=BC•CF. 如图,已知E为直线AD上一点,∠1=∠2,∠B=∠C,请写出图中一组相等的线段
如图,已知E为直线AD上一点,∠1=∠2,∠B=∠C,请写出图中一组相等的线段