题目内容
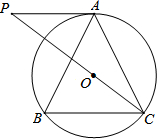 如图,⊙O是△ABC的外接圆,AB=AC,连结CO并延长交⊙O的切线AP于点P.
如图,⊙O是△ABC的外接圆,AB=AC,连结CO并延长交⊙O的切线AP于点P.(1)求证:∠APC=∠BCP;
(2)若sin∠APC=
| 3 |
| 5 |
考点:切线的性质,相似三角形的判定与性质
专题:
分析:(1)连结AO并延长交BC于D、
于E,利用切线的性质和垂径定理即可证明AP∥BC,进而可证明:∠APC=∠BCP;
(2)设OA=3k,OP=5k,则OC=OA=3k,因为BC∥AP,所以△PAO∽△CDO,根据相似三角形的性质:对应边的比值相等即可求出AP的长.
 |
| BC |
(2)设OA=3k,OP=5k,则OC=OA=3k,因为BC∥AP,所以△PAO∽△CDO,根据相似三角形的性质:对应边的比值相等即可求出AP的长.
解答:(1)证明:连结AO并延长交BC于D、
于E,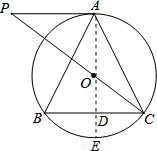
∵AP切⊙O于点A,
∴AP⊥AE,
∵AB=AC,
∴
=
,
∴AE⊥BC,
∴AP∥BC,
∴∠APC=∠BCP,
(2)解:∵AE⊥BC,
∴CD=
BC=2,
∵sin∠APC=
=
,
∴设OA=3k,OP=5k,则OC=OA=3k,
∵BC∥AP,
∴△PAO∽△CDO,
∴
=
,
∴
=
,
∴PA=
.
 |
| BC |

∵AP切⊙O于点A,
∴AP⊥AE,
∵AB=AC,
∴
 |
| AB |
 |
| AC |
∴AE⊥BC,
∴AP∥BC,
∴∠APC=∠BCP,
(2)解:∵AE⊥BC,
∴CD=
| 1 |
| 2 |
∵sin∠APC=
| AO |
| PO |
| 3 |
| 5 |
∴设OA=3k,OP=5k,则OC=OA=3k,
∵BC∥AP,
∴△PAO∽△CDO,
∴
| PA |
| CD |
| PO |
| CO |
∴
| PA |
| 2 |
| 5k |
| 3k |
∴PA=
| 10 |
| 3 |
点评:本题利用了垂径定理的推论、切线的性质、相似三角形的判定和性质、锐角三角函数,题目的难度中等,是常见中考题型.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
对于一组统计数据:2,3,5,6,4,4,下列说法错误的是( )
| A、众数是4 | B、中位数是4 |
| C、平均数是4 | D、方差是4 |
 如图,把一张长方形纸条ABCD沿EF折叠,若∠1=50°,则∠AEG=
如图,把一张长方形纸条ABCD沿EF折叠,若∠1=50°,则∠AEG=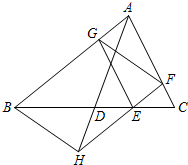 已知:如图,在△ABC中,AD是边BC上的中线,点E在线段DC上,EF∥AB交边AC于点F,EG∥AC交边AB于点G,FE的延长线与AD的延长线交于点H.
已知:如图,在△ABC中,AD是边BC上的中线,点E在线段DC上,EF∥AB交边AC于点F,EG∥AC交边AB于点G,FE的延长线与AD的延长线交于点H.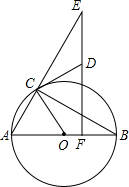 如图,AB为⊙O的直径,∠ABC=30°,ED⊥AB于点F,CD切⊙O于点C,交EF于点D.
如图,AB为⊙O的直径,∠ABC=30°,ED⊥AB于点F,CD切⊙O于点C,交EF于点D.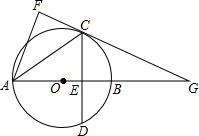 如图,在⊙O中,直径AB垂直于弦CD,垂足为E,连AC,将△ACE沿AC翻折得到△ACF,直线CF与直线AB相交于G.
如图,在⊙O中,直径AB垂直于弦CD,垂足为E,连AC,将△ACE沿AC翻折得到△ACF,直线CF与直线AB相交于G.