题目内容
对于二次函数y=x2-2mx-3,有下列说法:
①它的图象与x轴有两个交点;
②如果当x≤1时y随x的增大而减小,则m=1;
③如果x=3时的函数值与x=2013时的函数值相等,则该函数图象的对称轴是直线x=1005.
其中正确的说法是( )
①它的图象与x轴有两个交点;
②如果当x≤1时y随x的增大而减小,则m=1;
③如果x=3时的函数值与x=2013时的函数值相等,则该函数图象的对称轴是直线x=1005.
其中正确的说法是( )
| A、只有① | B、只有①② |
| C、只有②③ | D、只有①③ |
考点:二次函数的性质
专题:
分析:根据判别式的大小,可判断①,根据a的大小,对称轴的位置,可判断②,根据根据函数值相等,可判断③.
解答:解:①y=x2-2mx-3,当x2-2mx-3=0时,△=b2-4ac=(-2m)2-4×1×(-3)=4m2+12>0,它的图象与x轴有两个交点,故①正确;
②y=x2-2mx-3,a=1>0开口向上,x=-
=-
=1,m=1,对称轴的左侧,y随x的增大而减小,故②正确;
③x=3时的函数值与x=2013时的函数值相等,则该函数图象的对称轴是直线x=1008,故③错误;
故选:B.
②y=x2-2mx-3,a=1>0开口向上,x=-
| b |
| 2a |
| -2m |
| 2 |
③x=3时的函数值与x=2013时的函数值相等,则该函数图象的对称轴是直线x=1008,故③错误;
故选:B.
点评:本题考查了二次函数的性质,a>0是开口向上,对称轴的左侧,y随x的增大而减小;对称轴的右侧,y随x的增大而增大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
(-2)3的相反数是( )
| A、-6 | B、8 | C、-8 | D、6 |
 如图,在平行四边形ABCD中,下列结论中错误的是( )
如图,在平行四边形ABCD中,下列结论中错误的是( )| A、∠1=∠2 |
| B、∠BAD=∠BCD |
| C、AB=CD |
| D、AC=BC |
对于一组统计数据:2,3,5,6,4,4,下列说法错误的是( )
| A、众数是4 | B、中位数是4 |
| C、平均数是4 | D、方差是4 |
关于x的分式方程
=1,下列说法正确的是( )
| a |
| x+3 |
| A、方程的解是x=a-3 |
| B、当a>3时,方程的解是正数 |
| C、当a<3时,方程的解为负数 |
| D、以上答案都正确 |
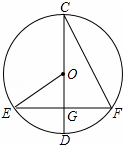 如图,⊙O的直径CD⊥EF,∠OEG=28°,则∠DCF=
如图,⊙O的直径CD⊥EF,∠OEG=28°,则∠DCF=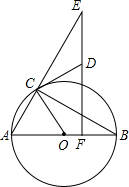 如图,AB为⊙O的直径,∠ABC=30°,ED⊥AB于点F,CD切⊙O于点C,交EF于点D.
如图,AB为⊙O的直径,∠ABC=30°,ED⊥AB于点F,CD切⊙O于点C,交EF于点D.