题目内容
16. 如图,在半径为10cm的⊙O中,弦AB的长为10cm,求点O到弦AB的距离及弧AB的长度.
如图,在半径为10cm的⊙O中,弦AB的长为10cm,求点O到弦AB的距离及弧AB的长度.
分析 过点O作OC⊥AB于点C,由在半径为10cm的⊙O中,弦AB的长为10cm,可得△OAB是等边三角形,继而求得∠AOB的度数,然后由三角函数的性质,求得点O到AB的距离,由弧长公式求出弧AB的长度即可.
解答 解:过点O作OC⊥AB于点C,如图所示:
∵OA=OB=AB=10cm,
∴△OAB是等边三角形,
∴∠AOB=60°,
∴OC=OA•sin60°=10×$\frac{\sqrt{3}}{2}$=5$\sqrt{3}$(cm),$\widehat{AB}$的长度=$\frac{60×π×10}{180}$=$\frac{10π}{3}$;
即点O到弦AB的距离为5$\sqrt{3}$cm,弧AB的长度为$\frac{10π}{3}$cm.
点评 此题考查了垂径定理、等边三角形的判定与性质、三角函数、弧长公式.熟练掌握垂径定理,证明△OAB是等边三角形是解决问题的关键.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
7.若m是任意实数,则点A(m,3-m)一定不在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
11.将关于x的方程x2-4x-2=0进行配方,正确的是( )
| A. | (x-2)2=2 | B. | (x+2)2=2 | C. | (x+2)2=6 | D. | (x-2)2=6 |
8.下列根式中能与$\sqrt{2}$合并的二次根式为( )
| A. | $\sqrt{24}$ | B. | $\sqrt{12}$ | C. | $\sqrt{\frac{3}{2}}$ | D. | $\sqrt{18}$ |
 如图,AD∥BE∥CF,直线m,n与这三条平行线分别交于点A、B、C和点D、E、F,已知AB=5,BC=10,DE=4,则EF的长为( )
如图,AD∥BE∥CF,直线m,n与这三条平行线分别交于点A、B、C和点D、E、F,已知AB=5,BC=10,DE=4,则EF的长为( )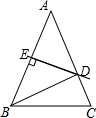 如图,△ABC中,AB=AC,AB的垂直平分线DE分别交AC、AB于点D、E.
如图,△ABC中,AB=AC,AB的垂直平分线DE分别交AC、AB于点D、E.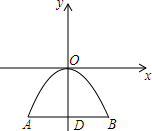 一座石拱桥的桥拱是近似的抛物线形.建立如图所示的坐标系,其函数关系式为
一座石拱桥的桥拱是近似的抛物线形.建立如图所示的坐标系,其函数关系式为