题目内容
1.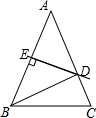 如图,△ABC中,AB=AC,AB的垂直平分线DE分别交AC、AB于点D、E.
如图,△ABC中,AB=AC,AB的垂直平分线DE分别交AC、AB于点D、E.(1)若∠A=50°,求∠CBD的度数;
(2)若AB=8,△CBD周长为13,求BC的长.
分析 (1)根据三角形内角和定理求出∠ABC=∠C=65°,根据线段垂直平分线的性质得到DA=DB,求出∠ABD的度数,计算即可;
(2)根据线段垂直平分线的性质和三角形的周长公式计算即可.
解答 解:(1)∵AB=AC,∠A=50°,
∴∠ABC=∠C=65°,
又∵DE垂直平分AB,
∴DA=DB,
∴∠ABD=∠A=50°,
∴∠DBC=15°;
(2)∵DE垂直平分AB,
∴DA=DB,
∴DB+DC=DA+DC=AC,
又∵AB=AC=8,△CBD周长为13,
∴BC=5.
点评 本题考查的是线段垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
6.若函数y=(k-1)x|k|+b+1是正比例函数,则k和b的值为( )
| A. | k=±1,b=-1 | B. | k=±1,b=0 | C. | k=1,b=-1 | D. | k=-1,b=-1 |
11.若a:b:c=2:3:4且a+b-c=6,则a-b+c=( )
| A. | 16 | B. | 17 | C. | 18 | D. | 19 |
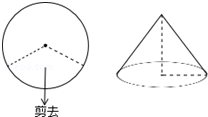 如图,圣诞节快到了,小雪准备在一块半径为9cm的 红布上剪掉三分之一圆周,然后用剩下的部分做成一个圣诞帽,则这个圣诞帽的高为3$\sqrt{5}$cm.
如图,圣诞节快到了,小雪准备在一块半径为9cm的 红布上剪掉三分之一圆周,然后用剩下的部分做成一个圣诞帽,则这个圣诞帽的高为3$\sqrt{5}$cm.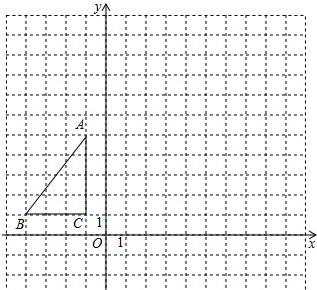 如图,在平面直角坐标系内,△ABC的顶点坐标分别为A(-1,5),B(-4,1),C(-1,1),将△ABC绕点A逆时针旋转90°,得到△AB′C′,点B,C的对应点分别为点B′,C′.
如图,在平面直角坐标系内,△ABC的顶点坐标分别为A(-1,5),B(-4,1),C(-1,1),将△ABC绕点A逆时针旋转90°,得到△AB′C′,点B,C的对应点分别为点B′,C′. 如图,在半径为10cm的⊙O中,弦AB的长为10cm,求点O到弦AB的距离及弧AB的长度.
如图,在半径为10cm的⊙O中,弦AB的长为10cm,求点O到弦AB的距离及弧AB的长度.