题目内容
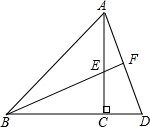 如图,BE是等腰△ABC的角平分线,∠C=90°,延长BC到D,使CD=CE,连结AD与BE的延长线交于F,求证:AE•AC=2AF2.
如图,BE是等腰△ABC的角平分线,∠C=90°,延长BC到D,使CD=CE,连结AD与BE的延长线交于F,求证:AE•AC=2AF2.考点:相似三角形的判定与性质
专题:证明题
分析:如图,连接CF;首先证明A、B、C、E四点共圆,得到∠AFB=∠ACB=90°,∠BFD+∠ACD=180,进而证明E、F、D、C四点共圆,得到AE•AC=AF•AD;证明AD=2AF,即可解决问题.
解答: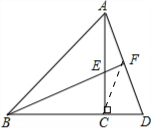 证明:连接CF;
证明:连接CF;
在△BCE和△ACD中,
,
∴△BCE≌△ACD(SAS),
∴∠EBC=∠FAC,
∴A、B、C、E四点共圆,
∴∠AFB=∠ACB=90°,∠BFD+∠ACD=180°,
∴E、F、D、C四点共圆,
∴AE•AC=AF•AD;
在△ABF与△DBF中,
,
∴△ABF≌△DBF(ASA),
∴AF=DF,AD=2AF,
∴AE•AC=2AF2.
 证明:连接CF;
证明:连接CF;在△BCE和△ACD中,
|
∴△BCE≌△ACD(SAS),
∴∠EBC=∠FAC,
∴A、B、C、E四点共圆,
∴∠AFB=∠ACB=90°,∠BFD+∠ACD=180°,
∴E、F、D、C四点共圆,
∴AE•AC=AF•AD;
在△ABF与△DBF中,
|
∴△ABF≌△DBF(ASA),
∴AF=DF,AD=2AF,
∴AE•AC=2AF2.
点评:该题主要考查了相似三角形的判定及其性质的应用问题;解题的关键是作辅助线,灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
下列命题中是假命题的是( )
| A、平行四边形的对边相等 |
| B、菱形的四条边相等 |
| C、矩形的对边平行且相等 |
| D、平行四边形的对角线相等 |
 如图,AB=AC,点D、E分别在线段AB、AC上,连接BE、CD交于点0,∠B=∠C,求证:OB=OC.
如图,AB=AC,点D、E分别在线段AB、AC上,连接BE、CD交于点0,∠B=∠C,求证:OB=OC.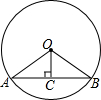 已知:如图,在半径为R的⊙O中,∠AOB=2α,OC⊥AB于C点.
已知:如图,在半径为R的⊙O中,∠AOB=2α,OC⊥AB于C点.  如图,在△ABC中,CD是∠C的角平分线,∠A=2∠B,求证:BC=AC+AD.
如图,在△ABC中,CD是∠C的角平分线,∠A=2∠B,求证:BC=AC+AD. 如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于D,DM⊥AC交AC的延长线于M,连接CD,且CD=BD.下列结论:
如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于D,DM⊥AC交AC的延长线于M,连接CD,且CD=BD.下列结论: 已知D,E分别为△ABC的边BC、AC中点,BE与AD交于点G,EF∥BC交AD于F,则AF:FG=
已知D,E分别为△ABC的边BC、AC中点,BE与AD交于点G,EF∥BC交AD于F,则AF:FG= 如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=1,BC=3,CD=4,求证:以CD为直径的圆与AB相切.
如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=1,BC=3,CD=4,求证:以CD为直径的圆与AB相切.