题目内容
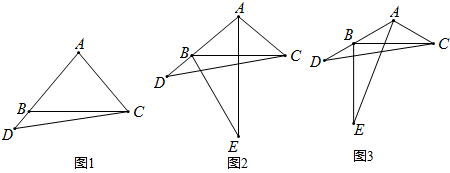
 如图,AB=AC,点D、E分别在线段AB、AC上,连接BE、CD交于点0,∠B=∠C,求证:OB=OC.
如图,AB=AC,点D、E分别在线段AB、AC上,连接BE、CD交于点0,∠B=∠C,求证:OB=OC.考点:全等三角形的判定与性质
专题:证明题
分析:易证△ABE≌△ACD,可得AE=AD,再根据AB=AC,可得BD=EC,即可证明△BOD≌△COE,即可解题.
解答:证明:在△ABE和△ACD中,
,
∴△ABE≌△ACD(ASA),
∴AE=AD,
∵AC=AB,
∴AC-AE=AB-AD,即BD=EC,
在△BOD和△COE中,
,
∴△BOD≌△COE(AAS),
∴OB=OC.
|
∴△ABE≌△ACD(ASA),
∴AE=AD,
∵AC=AB,
∴AC-AE=AB-AD,即BD=EC,
在△BOD和△COE中,
|
∴△BOD≌△COE(AAS),
∴OB=OC.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△BOD≌△COE是解题的关键.

练习册系列答案
相关题目
下列各数与2的和是0的是( )
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
 如图,在Rt△ABC中∠ABC=90°,BA=BC,P在△ABC的内部,且∠APB=135°,PA:PC=1:3,求PA:PB.
如图,在Rt△ABC中∠ABC=90°,BA=BC,P在△ABC的内部,且∠APB=135°,PA:PC=1:3,求PA:PB.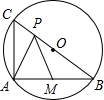 如图,BC为⊙O的直径,BC=2
如图,BC为⊙O的直径,BC=2 如图,每个小正方形的边长为1,剪一剪,拼成一个正方形,那么这个正方形的边长是
如图,每个小正方形的边长为1,剪一剪,拼成一个正方形,那么这个正方形的边长是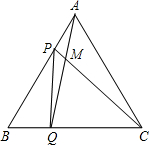 如图,点P、Q分别是边长是4cm的等边△ABC的边AB、BC上的动点,点P从顶点A出发沿着路线A→B→C→A做匀速运动,同时,点Q从顶点B出发,沿着路线B→C→A→B做匀速运动,且点P,Q的速度都为1cm/s,设运动时间为t秒
如图,点P、Q分别是边长是4cm的等边△ABC的边AB、BC上的动点,点P从顶点A出发沿着路线A→B→C→A做匀速运动,同时,点Q从顶点B出发,沿着路线B→C→A→B做匀速运动,且点P,Q的速度都为1cm/s,设运动时间为t秒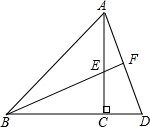 如图,BE是等腰△ABC的角平分线,∠C=90°,延长BC到D,使CD=CE,连结AD与BE的延长线交于F,求证:AE•AC=2AF2.
如图,BE是等腰△ABC的角平分线,∠C=90°,延长BC到D,使CD=CE,连结AD与BE的延长线交于F,求证:AE•AC=2AF2.