题目内容
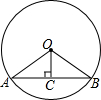 已知:如图,在半径为R的⊙O中,∠AOB=2α,OC⊥AB于C点.
已知:如图,在半径为R的⊙O中,∠AOB=2α,OC⊥AB于C点. (1)求弦AB的长及弦心距;
(2)求⊙O的内接正n边形的边长an及边心距rn.
考点:正多边形和圆
专题:
分析:(1)证明∠AOC=α,AC=BC;根据边角关系证明AC=Rsinα,OC=Rcosα,问题即可解决.
(2)求出α=
,借助(1)中的结论,即可解决问题.
(2)求出α=
| 180° |
| n |
解答: 解:(1)∵OA=OB,OC⊥AB,∠AOB=2α,
解:(1)∵OA=OB,OC⊥AB,∠AOB=2α,
∴∠AOC=α,AC=BC;
∵sinα=
,cosα=
,
∴AC=Rsinα,OC=Rcosα,
∴弦AB的长=2Rsinα,弦心距=Rcosα.
(2)如图,设AB、OC分别为⊙O的内接正n边形的边长an及边心距rn,
则∠AOB=
,即2α=
,
∴α=
,
∴an=2Rsin
,rn=Rcos
.
 解:(1)∵OA=OB,OC⊥AB,∠AOB=2α,
解:(1)∵OA=OB,OC⊥AB,∠AOB=2α,∴∠AOC=α,AC=BC;
∵sinα=
| AC |
| OA |
| OC |
| OA |
∴AC=Rsinα,OC=Rcosα,
∴弦AB的长=2Rsinα,弦心距=Rcosα.
(2)如图,设AB、OC分别为⊙O的内接正n边形的边长an及边心距rn,
则∠AOB=
| 360° |
| .n |
| 360° |
| n |
∴α=
| 180° |
| n |
∴an=2Rsin
| 180° |
| n |
| 180° |
| n |
点评:该题主要考查了正多边形和圆的性质及其应用问题;解题的关键是灵活运用有关定理来分析、判断;对求解运算能力、推理论证能力等均提出了一定的要求.

练习册系列答案
相关题目
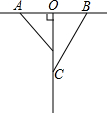 如图所示,AO=BO=50cm,OC是一条射线,OC⊥AB于点O,一只甲虫由点A以2cm/s的速度向B爬行,同时另一只甲虫由点O以3cm/s的速度沿OC方向爬行,是否存在这样的时刻,使两只甲虫与点O组成的三角形的面积为450cm2?若存在,请说明在什么时刻;若不存在,请说明理由.
如图所示,AO=BO=50cm,OC是一条射线,OC⊥AB于点O,一只甲虫由点A以2cm/s的速度向B爬行,同时另一只甲虫由点O以3cm/s的速度沿OC方向爬行,是否存在这样的时刻,使两只甲虫与点O组成的三角形的面积为450cm2?若存在,请说明在什么时刻;若不存在,请说明理由. 如图,在Rt△ABC中∠ABC=90°,BA=BC,P在△ABC的内部,且∠APB=135°,PA:PC=1:3,求PA:PB.
如图,在Rt△ABC中∠ABC=90°,BA=BC,P在△ABC的内部,且∠APB=135°,PA:PC=1:3,求PA:PB. 如图,每个小正方形的边长为1,剪一剪,拼成一个正方形,那么这个正方形的边长是
如图,每个小正方形的边长为1,剪一剪,拼成一个正方形,那么这个正方形的边长是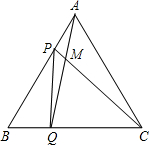 如图,点P、Q分别是边长是4cm的等边△ABC的边AB、BC上的动点,点P从顶点A出发沿着路线A→B→C→A做匀速运动,同时,点Q从顶点B出发,沿着路线B→C→A→B做匀速运动,且点P,Q的速度都为1cm/s,设运动时间为t秒
如图,点P、Q分别是边长是4cm的等边△ABC的边AB、BC上的动点,点P从顶点A出发沿着路线A→B→C→A做匀速运动,同时,点Q从顶点B出发,沿着路线B→C→A→B做匀速运动,且点P,Q的速度都为1cm/s,设运动时间为t秒 如图,点C在线段AB上.
如图,点C在线段AB上.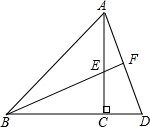 如图,BE是等腰△ABC的角平分线,∠C=90°,延长BC到D,使CD=CE,连结AD与BE的延长线交于F,求证:AE•AC=2AF2.
如图,BE是等腰△ABC的角平分线,∠C=90°,延长BC到D,使CD=CE,连结AD与BE的延长线交于F,求证:AE•AC=2AF2.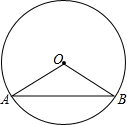 如图,弦AB把圆周分成1:2两部分,已知⊙O的半径为1,求弦AB的长.
如图,弦AB把圆周分成1:2两部分,已知⊙O的半径为1,求弦AB的长.