题目内容
19．
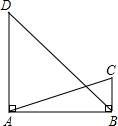如图，已知∠ABC=∠BAD=90°，AC=13，BC=5，AD=16，求BD的长．
分析 在Rt△ABC中根据勾股定理求出AB的长，再求出BD的长即可．
解答 解：∵∠ABC=90°，AC=13，BC=5，
∴AB=$\sqrt{{AC}^{2}-{BC}^{2}}$=$\sqrt{{13}^{2}-{5}^{2}}$=12．
∵∠BAD=90°，AD=16，
∴BD=$\sqrt{{AD}^{2}+{AB}^{2}}$=$\sqrt{{16}^{2}+{12}^{2}}$=20．
点评 本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键
练习册系列答案
阅读快车系列答案
相关题目
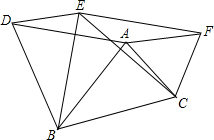如图，在△ABC中，AB=4，AC=3，BC=5，以三边为边，在BC的同侧分别作三个等边三角形即△ABD，△BCE，△ACF．