题目内容
12.下列条件中,能判断△ABC∽△A′B′C′的有( )①∠A=45°,AB=24,AC=30,∠A′=45°,A′B′=32,A′C′=40;
②AB=6,BC=7.5,AC=12,A′B′=10,B′C′=12.5,A′C′=20;
③∠A=47°,AB=1.5,AC=2,∠A′=47°,A′B′=2.8,B′C′=2.1.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 根据①②③分别判定△ABC∽△A′B′C′,计算成立的个数即可解题.
解答 解:①中,利用“两边及夹角”可以判断△ABC∽△A′B′C′,故①满足条件;
②中,∵$\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$=$\frac{BC}{B′C′}$,∴△ABC∽△A′B′C′,故②满足条件;
③中,∵$\frac{AB}{A′B′}$≠$\frac{AC}{A′C′}$,∴△ABC与△A′B′C′不相似,故③不满足条件,
故有2个可以判定△ABC∽△A′B′C′,
故选:B.
点评 本题考查了相似三角形的判定,考查了相似三角形各对应边长比例均相等的性质.

练习册系列答案
相关题目
20.把一个正方形的一边增加2cm,另一边增加1cm,得到的矩形面积的2倍比正方形的面积多11cm2.设这个正方形的边长为x cm,依题意可得方程为( )
| A. | (x+2)(x+1)=2x2+14 | B. | 2(x+2)(x+1)=x2+11 | C. | 2(x-2)(x-1)=x2+11 | D. | (x-2)(x-1)=2x2+11 |
7. 如图,若△ABC∽△ACD,∠A=60°,∠ACD=40°,则∠BCD的度数为( )
如图,若△ABC∽△ACD,∠A=60°,∠ACD=40°,则∠BCD的度数为( )
 如图,若△ABC∽△ACD,∠A=60°,∠ACD=40°,则∠BCD的度数为( )
如图,若△ABC∽△ACD,∠A=60°,∠ACD=40°,则∠BCD的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 30°或50° |
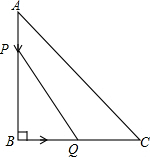 如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=3cm,点P从点A开始出发沿AB向点B以1cm/s的速度移动,点Q从点B开始沿BC向点C以2cm/s的速度移动,如果点P、Q分别从A、B同时出发,当P、Q到达B、C时停止运动.求:几秒中后,P、Q间的距离为4$\sqrt{2}$cm?
如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=3cm,点P从点A开始出发沿AB向点B以1cm/s的速度移动,点Q从点B开始沿BC向点C以2cm/s的速度移动,如果点P、Q分别从A、B同时出发,当P、Q到达B、C时停止运动.求:几秒中后,P、Q间的距离为4$\sqrt{2}$cm? 如图,直线l1的解析表达式为:y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,点B的坐标为(3,-$\frac{3}{2}$)直线l1,l2交于点C.
如图,直线l1的解析表达式为:y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,点B的坐标为(3,-$\frac{3}{2}$)直线l1,l2交于点C.