题目内容
14.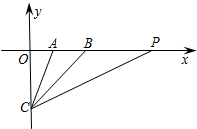 如图,在平面直角坐标系中,A(2,0),B(4,0),C(0,-4),CB平分∠ACP,则直线PC的解析式为y=$\frac{1}{2}$x-4.
如图,在平面直角坐标系中,A(2,0),B(4,0),C(0,-4),CB平分∠ACP,则直线PC的解析式为y=$\frac{1}{2}$x-4.
分析 由题意可得∠OBC=∠OCB=45°,证明∠OPC=∠OCA,然后可得△OPC∽△OCA,求出OP的长度,得出点P的坐标,利用待定系数法可确定直线PC的解析式.
解答 解:∵B(4,0),C(0,-4),
∴OB=OC=4,
∴∠OBC=∠OCB=45°,
∵∠OPC+∠BCP=∠OBC=45°,∠OCA+∠ACB=45°,CB平分∠ACP,
∴∠OPC=∠OCA,
∴△OPC∽△OCA,
∴$\frac{OA}{OC}$=$\frac{OC}{OP}$,即$\frac{2}{4}$=$\frac{4}{OP}$,
∴OP=8,
∴点P的坐标为(8,0),
设直线CP的解析式为:y=kx+b,
则$\left\{\begin{array}{l}{8k+b=0}\\{b=-4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=-4}\end{array}\right.$,
∴直线CP的解析式为y=$\frac{1}{2}$x-4.
故答案为:y=$\frac{1}{2}$x-4.
点评 此题考查待定系数法求函数解析式,相似三角形的判定与性质,等腰直角三角形的性质,解答本题的关键△OPC∽△OCA的证明,得出OP的长度.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
19. 如图,AB是⊙0的直径,点C、D在⊙0上,∠BOD=110°,AD∥OC,则∠AOC=( )
如图,AB是⊙0的直径,点C、D在⊙0上,∠BOD=110°,AD∥OC,则∠AOC=( )
 如图,AB是⊙0的直径,点C、D在⊙0上,∠BOD=110°,AD∥OC,则∠AOC=( )
如图,AB是⊙0的直径,点C、D在⊙0上,∠BOD=110°,AD∥OC,则∠AOC=( )| A. | 70° | B. | 60° | C. | 50° | D. | 55° |
4.关于x的方程x2-2x+c=0有两个相等的实数根,则c的值为( )
| A. | 1 | B. | -1 | C. | 4 | D. | -4 |
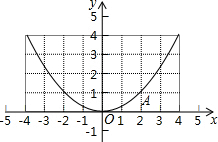 如图是一个二次函数的图象,顶点是原点O,且过点A(2,1),
如图是一个二次函数的图象,顶点是原点O,且过点A(2,1),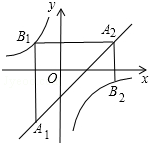 如图,已知点A1,A2,…,An均在直线y=x-1上,点B1,B2,…,Bn均在双曲线y=-$\frac{1}{x}$ 上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2016=$\frac{1}{2}$.
如图,已知点A1,A2,…,An均在直线y=x-1上,点B1,B2,…,Bn均在双曲线y=-$\frac{1}{x}$ 上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2016=$\frac{1}{2}$.