题目内容
8.计算:(-3)0-$\root{3}{27}$+|1-$\sqrt{2}$|+$\sqrt{2}$×$\sqrt{6}$+($\sqrt{3}$+$\sqrt{2}$)-1.分析 直接利用负整数指数幂的性质以及零指数幂的性质和绝对值的性质分别化简求出答案.
解答 解:(-3)0-$\root{3}{27}$+|1-$\sqrt{2}$|+$\sqrt{2}$×$\sqrt{6}$+($\sqrt{3}$+$\sqrt{2}$)-1
=1-3+$\sqrt{2}$-1+2$\sqrt{3}$+$\sqrt{3}$-$\sqrt{2}$
=3$\sqrt{3}$-3.
点评 此题主要考查了负整数指数幂的性质以及零指数幂的性质和绝对值的性质,正确化简各数是解题关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
18.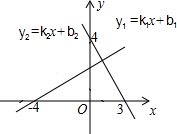 如图,直线y1=k1x+b1与坐标轴交于点(-4,0)和(0,2.9);直线y2=k2x+b2与坐标轴交于点(3,0)和(0,4).不等式组$\left\{\begin{array}{l}{{k}_{1}x+{b}_{1}>0}\\{{k}_{2}x+{b}_{2}>0}\end{array}\right.$的解集是( )
如图,直线y1=k1x+b1与坐标轴交于点(-4,0)和(0,2.9);直线y2=k2x+b2与坐标轴交于点(3,0)和(0,4).不等式组$\left\{\begin{array}{l}{{k}_{1}x+{b}_{1}>0}\\{{k}_{2}x+{b}_{2}>0}\end{array}\right.$的解集是( )
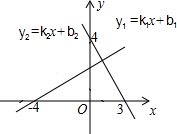 如图,直线y1=k1x+b1与坐标轴交于点(-4,0)和(0,2.9);直线y2=k2x+b2与坐标轴交于点(3,0)和(0,4).不等式组$\left\{\begin{array}{l}{{k}_{1}x+{b}_{1}>0}\\{{k}_{2}x+{b}_{2}>0}\end{array}\right.$的解集是( )
如图,直线y1=k1x+b1与坐标轴交于点(-4,0)和(0,2.9);直线y2=k2x+b2与坐标轴交于点(3,0)和(0,4).不等式组$\left\{\begin{array}{l}{{k}_{1}x+{b}_{1}>0}\\{{k}_{2}x+{b}_{2}>0}\end{array}\right.$的解集是( )| A. | x>-4 | B. | x<3 | C. | -4<x<3 | D. | x<-4或x>3 |
16.已知正比例函数y=(m-3)x的图象过第二、四象限,则m的取值范围是( )
| A. | m≥3 | B. | m>3 | C. | m≤3 | D. | m<3 |
3.已知关于x的方程x2-2x+a=0有两个相等的实数根,则a的值为( )
| A. | -1 | B. | 0 | C. | 2 | D. | 1 |
20.一组数据1、2、3、4、5、15的平均数和中位数分别是( )
| A. | 5、5 | B. | 5、4 | C. | 5、3.5 | D. | 5、3 |
17.实数n、m是连续整数,如果$n<\sqrt{26}<m$,那么m+n的值是( )
| A. | 7 | B. | 9 | C. | 11 | D. | 13 |
 利用一面墙(墙的长度为24m),另三边用用58m长的篱笆围成一个面积为200m2的矩形场地,求矩形的长和宽.
利用一面墙(墙的长度为24m),另三边用用58m长的篱笆围成一个面积为200m2的矩形场地,求矩形的长和宽.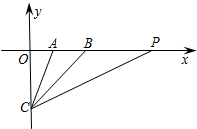 如图,在平面直角坐标系中,A(2,0),B(4,0),C(0,-4),CB平分∠ACP,则直线PC的解析式为y=$\frac{1}{2}$x-4.
如图,在平面直角坐标系中,A(2,0),B(4,0),C(0,-4),CB平分∠ACP,则直线PC的解析式为y=$\frac{1}{2}$x-4.