题目内容
2.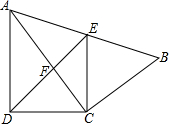 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,(1)求证:AC2=AB•AD;
(2)求证:CE∥AD;
(3)若AD=5,AB=8,求$\frac{AC}{AF}$的值.
分析 (1)根据两组对角对应相等的两个三角形相似证明即可;
(2)根据直角三角形的性质得到CE=BE=AE,根据等腰三角形的性质得到∠EAC=∠ECA,根据平行线的判定定理证明即可;
(3)证明△AFD∽△CFE,根据相似三角形的性质定理列出比例式,解答即可.
解答 (1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴AD:AC=AC:AB,
∴AC2=AB•AD;
(2)证明:∵E为AB的中点,
∴CE=BE=AE,
∴∠EAC=∠ECA,
∵∠DAC=∠CAB,
∴∠DAC=∠ECA,
∴CE∥AD;
(3)解:∵CE∥AD,
∴△AFD∽△CFE,
∴AD:CE=AF:CF,
∵CE=AB,
∴CE=×8=4,
∵AD=5,
∴$\frac{AF}{CF}$=$\frac{5}{4}$,
∴$\frac{AC}{AF}$=$\frac{9}{5}$.
点评 本题考查的是相似三角形的判定和性质、平行线的判定,掌握相似三角形的判定定理和性质定理是解题的关键.

练习册系列答案
相关题目
 请将数轴补全,然后把数-4,1,0,-|-1$\frac{1}{2}}$|,-(-5)表示在数轴上,并按从小到大的顺序,从左到右串个糖葫芦,把数填在“○”内.
请将数轴补全,然后把数-4,1,0,-|-1$\frac{1}{2}}$|,-(-5)表示在数轴上,并按从小到大的顺序,从左到右串个糖葫芦,把数填在“○”内.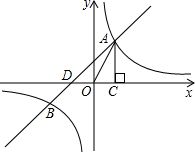 如图,已知反比例函数y1=$\frac{{k}_{1}}{x}$(k1>0)与一次函数y2=k2x+1(k2≠0)的图象交于A,B两点,AC⊥x轴于点C.若△OAC的面积为1,且AC=2OC.
如图,已知反比例函数y1=$\frac{{k}_{1}}{x}$(k1>0)与一次函数y2=k2x+1(k2≠0)的图象交于A,B两点,AC⊥x轴于点C.若△OAC的面积为1,且AC=2OC. 求抛物线y=x2-2x的对称轴和顶点坐标,并画出图象.
求抛物线y=x2-2x的对称轴和顶点坐标,并画出图象. 如图△ABC中,AB=AC=5,BC=3,DE是AB的中垂线,分别交AB,AC于点E,D,则△DBC的周长为8.
如图△ABC中,AB=AC=5,BC=3,DE是AB的中垂线,分别交AB,AC于点E,D,则△DBC的周长为8.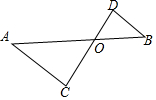 如图,已知△OAC∽△OBD,OA=4,AC=2,OB=2,∠C=∠D.求:
如图,已知△OAC∽△OBD,OA=4,AC=2,OB=2,∠C=∠D.求: