题目内容
11.已知关于x的一元二次方程x2-(m-2)x+$\frac{1}{2}$m-3=0(1)求证:无论m取什么实数时,这个方程总有两个不相等的实数根;
(2)如果方程的两个实数根为x1,x2,且2x1+x2=m+1,求m的值.
分析 (1)根据判别式△=(m-3)2+3>0,即可得到结果;
(2)根据根与系数的关系,把两根之和代入满足的等式,得到x1,再把x1代入方程可以求出m的值.
解答 解:(1)∵△=(m-2)2-4×($\frac{1}{2}$m-3)=(m-3)2+3>0,
∴无论m取什么实数值,这个方程总有两个不相等的实数根;
(2)解:x1+x2=m-2,
2x1+x2=x1+(x1+x2)=m+1,
∴x1=m+1+2-m=3,
把x1代入方程有:
9-3(m-2)+$\frac{1}{2}$m-3=0
解得m=$\frac{24}{5}$.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程的根与系数的关系.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
6.某自行车厂一周计划生产1400辆自行车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出入.表是某周的生产情况(超产为正、减产为负):
(1)根据记录可知前三天共生产多少辆;
(2)产量最多的一天比产量最少的一天多生产多少辆;
(3)该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +4 | -2 | -5 | +13 | -11 | +17 | -9 |
(2)产量最多的一天比产量最少的一天多生产多少辆;
(3)该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?
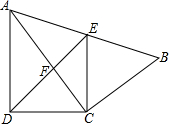 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,