题目内容
12.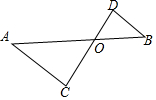 如图,已知△OAC∽△OBD,OA=4,AC=2,OB=2,∠C=∠D.求:
如图,已知△OAC∽△OBD,OA=4,AC=2,OB=2,∠C=∠D.求:(1)△OAC与△OBD的相似比;
(2)BD的长.
分析 (1)根据相似三角形的对应边成比例得到△OAC与△OBD的相似比是:$\frac{OA}{OB}$=2;
(2)根据相似三角形的对应边成比例来求BD的长度.
解答 解:(1)∵△OAC∽△OBD,∠C=∠D,
∴△OAC与△OBD的相似比是:$\frac{OA}{OB}$=2;
(2)∵△OAC∽△OBD,OA=4,AC=2,OB=2,∠C=∠D,
∴$\frac{OA}{OB}$=$\frac{AC}{BD}$,即$\frac{4}{2}$=$\frac{2}{BD}$,
则BD=1.
点评 本题考查对相似三角形性质的理解.(1)相似三角形周长的比等于相似比;(2)相似三角形面积的比等于相似比的平方;(3)相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
4.已知⊙O的半径为8cm,直线l上有一点B到圆心O的距离等于8cm,则直线l与⊙O的位置关系是( )
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 相交或相切 |
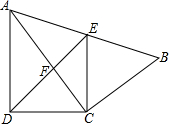 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,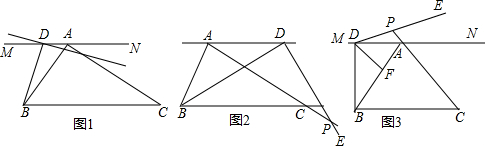
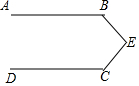 如图,∠B+∠E+∠C=360°,试判断AB与CD是否平行?请说明理由.
如图,∠B+∠E+∠C=360°,试判断AB与CD是否平行?请说明理由.