题目内容
10.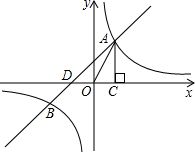 如图,已知反比例函数y1=$\frac{{k}_{1}}{x}$(k1>0)与一次函数y2=k2x+1(k2≠0)的图象交于A,B两点,AC⊥x轴于点C.若△OAC的面积为1,且AC=2OC.
如图,已知反比例函数y1=$\frac{{k}_{1}}{x}$(k1>0)与一次函数y2=k2x+1(k2≠0)的图象交于A,B两点,AC⊥x轴于点C.若△OAC的面积为1,且AC=2OC.(1)求反比例函数与一次函数的解析式;
(2)请直接写出点B的坐标;
(3)当x为何值时,反比例函数y1的值大于一次函数y2的值?
分析 (1)利用△OAC的面积求出点A的坐标,在将其代入反比例函数与一次函数的解析式即可.
(2)把(1)中所得的两个函数关系式联立成方程组求解即可.
(3)利用函数的图象求解:反比例函数y1的值大于一次函数y2的值,则在图象上反比例函数的图象位于一次函数的图象上方.
解答 解:(1)∵△OAC的面积为1,
∴$\frac{1}{2}$OC•AC=1,
又∵AC=2OC,
∴OC2=1,OC=±1(负值舍去)
∴点A的坐标为(1,2)
k1=2,2=k2+1,k2=1
∴反比例函数为:y=$\frac{2}{x}$,一次函数的解析式为:y=x+1
(2)解方程组$\left\{\begin{array}{l}{y=\frac{2}{x}}\\{y=x+1}\end{array}\right.$得:$\left\{\begin{array}{l}{{x}_{1}=1}\\{{y}_{1}=2}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-1}\\{{y}_{2=-2}}\end{array}\right.$
∴点B的坐标为(-1,-2)
(3)如图所示:
∵反比例函数y1的值大于一次函数y2的值,则在图象上反比例函数的图象位于一次函数的图象上方,
∴当x<-1或0<x<1时,反比例函数y1的值大于一次函数y2的值.
点评 本题考查了反比例函数与一次函数的交点问题,解题的关键是求出反比例函数与一次函数的交点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,E、F分别为线段AC上的两个点,且DE⊥AC于E,BF⊥AC于F,若AB=CD,AF=CE,BD交AC于点M.求证:MB=MD,ME=MF.
如图,E、F分别为线段AC上的两个点,且DE⊥AC于E,BF⊥AC于F,若AB=CD,AF=CE,BD交AC于点M.求证:MB=MD,ME=MF.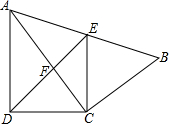 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,