Question

7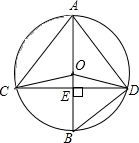．如图，⊙O的直径AB垂直于弦CD于E，连接AD、BD、OC、0D，且0D=5．
（1）若BD=6，求CD的长．
（2）若∠AD0：∠EDO=4：1，求∠A0C的度数．

Answer 1

分析 （1）首先根据垂径定理可得ED=$\frac{1}{2}$CD，然后利用勾股定理可得5²-x²=6²-（5-x）²，计算出x的值，再利用勾股定理计算出ED的长，进而可得答案；
（2）根据垂径定理可得$\widehat{AD}$=$\widehat{AC}$，$\widehat{CB}$=$\widehat{DB}$，然后计算出∠ODE的度数，再根据直角三角形两锐角互余可得∠DOE的度数，进而可得答案．

解答 解：（1）∵⊙O的直径AB垂直于弦CD，
∴ED=$\frac{1}{2}$CD，
∵0D=5，
∴BO=5，
设EO=x，则EB=5-x，
∴5²-x²=6²-（5-x）²，
解得：x=1.4，
∴ED=$\sqrt{D{O}^{2}-E{O}^{2}}$=4.8，
∴CD=9.6；

（2））∵AB是⊙O的直径，AB⊥CD，
∴$\widehat{AD}$=$\widehat{AC}$，$\widehat{CB}$=$\widehat{DB}$，
∴∠BAD=∠CDB，∠AOC=∠AOD，
∵AO=DO，
∴∠BAD=∠ADO，
∴∠CDB=∠ADO，
设∠ADO=4x，则∠CDB=4x．
由∠ADO：∠EDO=4：1，则∠EDO=x．
∵∠ADO+∠EDB+∠EDO=90°，
∴4x+4x+x=90°，
解得：x=10°，
∴∠EDO=10°，
∴∠EOD=80°，
∴∠AOD=100°，
∴∠AOC=100°．

点评 此题主要考查了垂径定理，以及勾股定理的应用，关键是掌握平分弦的直径平分这条弦，并且平分弦所对的两条弧．