题目内容
15.若|m+3|+(n+2)2=0,求:(1)求m,n的值;
(2)单项式$\frac{m{x}^{n+4}y}{9}$的系数和次数.
分析 (1)根据|m+3|+(n+2)2=0,可得m+3=0,n+2=0,据此分别求出m、n的值各是多少即可.
(2)把(1)中求出的m、n的值代入单项式$\frac{m{x}^{n+4}y}{9}$,求出它的系数和次数各是多少即可.
解答 解:(1)∵|m+3|+(n+2)2=0,
∴m+3=0,n+2=0,
∴m=-3,n=-2.
(2)∵$\frac{m{x}^{n+4}y}{9}$=$\frac{-3}{9}$x-2+4y=-$\frac{1}{3}$x2y,
∴单项式$\frac{m{x}^{n+4}y}{9}$的系数是-$\frac{1}{3}$,次数是:2+1=3.
点评 (1)此题主要考查了单项式问题,要熟练掌握,解答此题的关键是要明确:单项式中的数字因数叫做单项式的系数,一个单项式中所有字母的指数的和叫做单项式的次数.
(2)此题还考查了绝对值的非负性质的应用,以及偶次方的非负性质的应用,要熟练掌握,解答此题的关键是分别求出m、n的值各是多少.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
20.已知等腰三角形的两边长分别为4和6,则底边上的高的平方等于( )
| A. | 7 | B. | 7或41 | C. | 32 | D. | 32或7 |
 如图:
如图: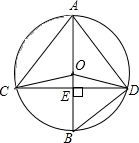 如图,⊙O的直径AB垂直于弦CD于E,连接AD、BD、OC、0D,且0D=5.
如图,⊙O的直径AB垂直于弦CD于E,连接AD、BD、OC、0D,且0D=5. 如图,点0是线段CD的中点,以点0为旋转中心,画出与已知图形成中心对称的图形.
如图,点0是线段CD的中点,以点0为旋转中心,画出与已知图形成中心对称的图形.