题目内容
解方程组或不等式组:
(1)
;
(2)
;
(3)
;
(4)
.
(1)
|
(2)
|
(3)
|
(4)
|
考点:解一元一次不等式组,解二元一次方程组
专题:
分析:(1)先用加减消元法求出x的值,再用代入消元法求出y的值即可;
(2)先用加减消元法求出y的值,再用代入消元法求出x的值即可;
(3)、(4)分别求出各不等式的解集,再求出其公共解集即可.
(2)先用加减消元法求出y的值,再用代入消元法求出x的值即可;
(3)、(4)分别求出各不等式的解集,再求出其公共解集即可.
解答:解:(1)
,①+②得,3x=15,解得x=5,把x=5代入②得,5+y=6,解得y=1,
故此不等式组的解集为
;
(2)
,①×2-②×3得,-19y=0,解得y=0,把y=0代入②得,2x+2=0,解得x=-1,
故此不等式组的解集为:
;
(3)
,由①得,y>-5,由②得,y<-2,
故不等式组的解集为:-5<y<-2;
(4)
,由①得,x>2,由②得,x<-6,
故不等式组无解.
|
故此不等式组的解集为
|
(2)
|
故此不等式组的解集为:
|
(3)
|
故不等式组的解集为:-5<y<-2;
(4)
|
故不等式组无解.
点评:本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
若x,y均为正整数,且2x+1•4y=128,则x+y的值为( )
| A、3 | B、5 |
| C、4或5 | D、3或4或5 |
 如图,一条直线上有两只蚂蚁,甲蚂蚁在点A处,乙蚂蚁在点B处,假设两只蚂蚁同时出发,爬行方向只能沿直线AB在“向左”或“向右”中随机选择,并且甲蚂蚁爬行的速度比乙蚂蚁快.
如图,一条直线上有两只蚂蚁,甲蚂蚁在点A处,乙蚂蚁在点B处,假设两只蚂蚁同时出发,爬行方向只能沿直线AB在“向左”或“向右”中随机选择,并且甲蚂蚁爬行的速度比乙蚂蚁快.
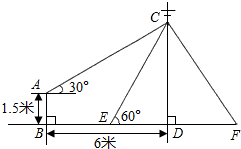 如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置高为1.5米的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长(结果保留小数点后一位,参考数据:
如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置高为1.5米的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长(结果保留小数点后一位,参考数据: