题目内容
若x，y均为正整数，且2x+1•4y=128，则x+y的值为（ ）
| A、3 | B、5 |
| C、4或5 | D、3或4或5 |
考点：幂的乘方与积的乘方,同底数幂的乘法
专题：
分析：先把2x+1•4y化为2x+1+2y，128化为27，得出x+1+2y=7，即x+2y=6因为x，y均为正整数，求出x，y，再求了出x+y．，
解答：解：∵2x+1•4y=2x+1+2y，27=128，
∴x+1+2y=7，即x+2y=6
∵x，y均为正整数，
∴
或
∴x+y=5或4，
故选：C．
∴x+1+2y=7，即x+2y=6
∵x，y均为正整数，
∴
|
|
∴x+y=5或4，
故选：C．
点评：本题主要考查了幂的乘方，同底数幂的乘法，解题的关键是化为相同底数的幂求解．
练习册系列答案
相关题目
某校九年级有560名学生参加了市教育局举行的读书活动，现随机调查了70名学生读书的数量，根据所得数据绘制了如图的条形统计图，请估计该校九年级学生在此次读书活动中共读书AC，BD是?ABCD的两条对角线，如果添加一个条件，使?ABCD为矩形，那么这个条件可以是（ ）
| A、AB=BC |
| B、AC=BD |
| C、AC⊥BD |
| D、AB⊥BD |
如图，已知矩形ABCD，R，P分别为DC，BC上的点，E，F分别是AP，RP的中点，当点P在BC上从点C向点B移动，点R从点D向点C移动时，那么下列结论成立的是（ ）| A、线段EF的长逐渐增大 |
| B、线段EF的长逐渐减小 |
| C、线段EF的长逐渐不变 |
| D、线段EF的长不能确定 |
方程组
的解x、y适合x＜0，y＞0，则a的取值范围为（ ）
|
A、a＞-
| ||
| B、a＞-1 | ||
C、-1＜a＜-
| ||
| D、a＜-1 |
下列说法正确的是（ ）
| A、“2014年长沙市初中毕业会考，这期间的每一天都是晴天”是必然事件 |
| B、垂直于弦的直径平分这条弦 |
| C、某同学连续10次抛掷质量均匀的硬币，3次正面向上，因此正面向上的概率是30% |
| D、对角线相等且互相垂直的四边形是正方形 |
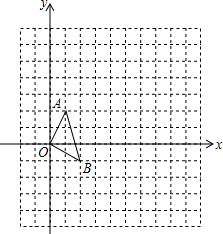如图，在12×12的正方形网格中，△OAB的顶点分别为O（0，0），A（1，2），B（2，-1）．