题目内容
已知:如图,AC⊥BD,BC=CE,AC=DC.求证:∠B+∠D=90°.


考点:全等三角形的判定与性质
专题:证明题
分析:求出∠ACB=∠DCE=90°,根据SAS证Rt△ACB≌Rt△DCE,推出∠A=∠D,根据三角形内角和定理得出即可.
解答:证明:∵AC⊥BD,
∴∠ACB=∠DCE=90°,
在Rt△ACB和Rt△DCE中,
∴Rt△ACB≌Rt△DCE(SAS),
∴∠A=∠D,
又∵在Rt△ACB中,∠A+∠B=90°,
∴∠B+∠D=90°.
∴∠ACB=∠DCE=90°,
在Rt△ACB和Rt△DCE中,
|
∴Rt△ACB≌Rt△DCE(SAS),
∴∠A=∠D,
又∵在Rt△ACB中,∠A+∠B=90°,
∴∠B+∠D=90°.
点评:本题考查了三角形内角和定理,全等三角形的性质和判定的应用,注意:全等三角形的对应角相等,对应边相等.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 如图,已知矩形ABCD,R,P分别为DC,BC上的点,E,F分别是AP,RP的中点,当点P在BC上从点C向点B移动,点R从点D向点C移动时,那么下列结论成立的是( )
如图,已知矩形ABCD,R,P分别为DC,BC上的点,E,F分别是AP,RP的中点,当点P在BC上从点C向点B移动,点R从点D向点C移动时,那么下列结论成立的是( )| A、线段EF的长逐渐增大 |
| B、线段EF的长逐渐减小 |
| C、线段EF的长逐渐不变 |
| D、线段EF的长不能确定 |
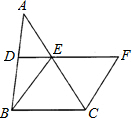 如图,△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
如图,△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.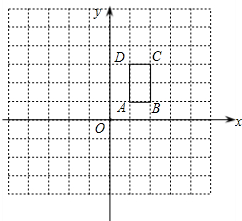 如图,矩形ABCD的顶点坐标分别为A(1,1),B(2,1),C(2,3),D(1,3).
如图,矩形ABCD的顶点坐标分别为A(1,1),B(2,1),C(2,3),D(1,3). 如图,在△ABC中,∠A=30°,∠B=50°,延长BC到D,则∠ACD=
如图,在△ABC中,∠A=30°,∠B=50°,延长BC到D,则∠ACD=