题目内容
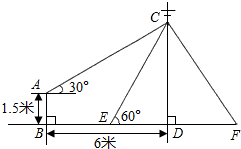 如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置高为1.5米的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长(结果保留小数点后一位,参考数据:
如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置高为1.5米的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长(结果保留小数点后一位,参考数据:| 2 |
| 3 |
考点:解直角三角形的应用-仰角俯角问题
专题:几何图形问题
分析:由题意可先过点A作AH⊥CD于H.在Rt△ACH中,可求出CH,进而CD=CH+HD=CH+AB,再在Rt△CED中,求出CE的长.
解答: 解:过点A作AH⊥CD,垂足为H,
解:过点A作AH⊥CD,垂足为H,
由题意可知四边形ABDH为矩形,∠CAH=30°,
∴AB=DH=1.5,BD=AH=6,
在Rt△ACH中,tan∠CAH=
,
∴CH=AH•tan∠CAH,
∴CH=AH•tan∠CAH=6tan30°=6×
(米),
∵DH=1.5,
∴CD=2
+1.5,
在Rt△CDE中,
∵∠CED=60°,sin∠CED=
,
∴CE=
=4+
≈5.7(米),
答:拉线CE的长约为5.7米.
 解:过点A作AH⊥CD,垂足为H,
解:过点A作AH⊥CD,垂足为H,由题意可知四边形ABDH为矩形,∠CAH=30°,
∴AB=DH=1.5,BD=AH=6,
在Rt△ACH中,tan∠CAH=
| CH |
| AH |
∴CH=AH•tan∠CAH,
∴CH=AH•tan∠CAH=6tan30°=6×
| ||
| 3 |
∵DH=1.5,
∴CD=2
| 3 |
在Rt△CDE中,
∵∠CED=60°,sin∠CED=
| CD |
| CE |
∴CE=
| CD |
| sin60° |
| 3 |
答:拉线CE的长约为5.7米.
点评:此题主要考查解直角三角形的应用.要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
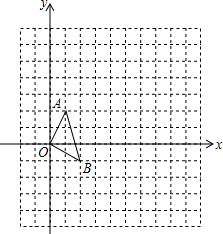 如图,在12×12的正方形网格中,△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).
如图,在12×12的正方形网格中,△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).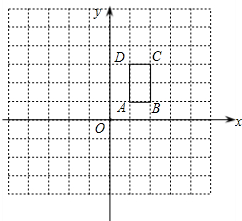 如图,矩形ABCD的顶点坐标分别为A(1,1),B(2,1),C(2,3),D(1,3).
如图,矩形ABCD的顶点坐标分别为A(1,1),B(2,1),C(2,3),D(1,3).