题目内容
如图，以△ABC的边AB为直径作⊙O，分别交AC、BC于点D、E，过点D作DF⊥BC于F点，D为 |
| AE |
考点：切线的判定
专题：证明题
分析：如图，作辅助线；证明AE∥DF；证明OD⊥AE，此为解题的关键性结论；即可解决问题．
解答：
证明：如图，连接AE、OD；
∵AB为⊙O的直径，
∴AE⊥BC，而DF⊥BC，
∴AE∥DF；
∵D为
中点，
∴OD⊥AE，
∴OD⊥DF，
即DF为⊙O的切线．
证明：如图，连接AE、OD；∵AB为⊙O的直径，
∴AE⊥BC，而DF⊥BC，
∴AE∥DF；
∵D为
|
| AE |
∴OD⊥AE，
∴OD⊥DF，
即DF为⊙O的切线．
点评：该题主要考查了圆的切线的判定问题；同时还考查了垂径定理、圆周角定理及其推论等几何知识点；解题的关键是作辅助线．
练习册系列答案
相关题目
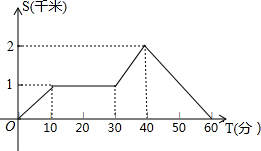星期天晚饭后，小丽的爸爸从家里出去散步，如图描述了她爸爸散步过程中离家的距离（km）与散步所用的时间（min）之间的函数关系，依据图象，下面描述符合小丽爸爸散步情景的是（ ）| A、从家出发，休息一会，就回家 |
| B、从家出发，一直散步（没有停留），然后回家 |
| C、从家出发，休息一会，返回用时20分钟 |
| D、从家出发，休息一会，继续行走一段，然后回家 |
用科学记数法表示9 270 000正确的是（ ）
| A、9.27×106 |
| B、9.27×105 |
| C、9.27×104 |
| D、927×103 |
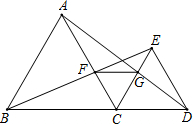如图，已知点C在线段BD上，在BD的同侧作正△CDE、正△ABC，AC交BE于F，AD交CE于G，连接FG，在这个图形中，不在标注其它字母和添加任何辅助线，由这些条件可推出哪些结论？
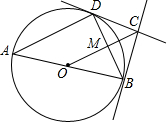如图，AB为⊙O的直径，BC⊥AB，OC过BD中点M，求证：CD是⊙O的切线．
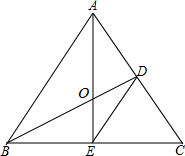如图，△ABC是等边三角形，BD⊥AC，AE⊥BC，垂足分别为D、E，AE、BD相交于点O，连接DE．