题目内容
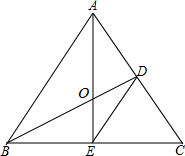 如图,△ABC是等边三角形,BD⊥AC,AE⊥BC,垂足分别为D、E,AE、BD相交于点O,连接DE.
如图,△ABC是等边三角形,BD⊥AC,AE⊥BC,垂足分别为D、E,AE、BD相交于点O,连接DE.(1)判断△CDE的形状,并说明理由.
(2)若AO=12,求OE的长.
考点:等边三角形的判定与性质
专题:
分析:(1)证明∠C=60°,CD=CE,即可解决问题.
(2)证明AO=2OE,即可解决问题.
(2)证明AO=2OE,即可解决问题.
解答: 解:(1)∵△ABC是等边三角形,且BD⊥AC,AE⊥BC,
解:(1)∵△ABC是等边三角形,且BD⊥AC,AE⊥BC,
∴∠C=60°,CE=
BC,CD=
AC;而BC=AC,
∴CD=CE,△CDE是等边三角形.
(2)由(1)知:AE、BD分别是△ABC的中线,
∴AO=2OE,而AO=12,
∴OE=6.
 解:(1)∵△ABC是等边三角形,且BD⊥AC,AE⊥BC,
解:(1)∵△ABC是等边三角形,且BD⊥AC,AE⊥BC,∴∠C=60°,CE=
| 1 |
| 2 |
| 1 |
| 2 |
∴CD=CE,△CDE是等边三角形.
(2)由(1)知:AE、BD分别是△ABC的中线,
∴AO=2OE,而AO=12,
∴OE=6.
点评:该题主要考查了等边三角形的判定及其性质的应用问题;应牢固掌握正方形的判定及其性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC与△A′B′C′中,AB:AC=A′B′:A′C′,∠B=∠B′,则这两个三角形( )
| A、相似,但不全等 |
| B、全等或相似 |
| C、不相似 |
| D、无法判断是否相似 |
 如图,以△ABC的边AB为直径作⊙O,分别交AC、BC于点D、E,过点D作DF⊥BC于F点,D为
如图,以△ABC的边AB为直径作⊙O,分别交AC、BC于点D、E,过点D作DF⊥BC于F点,D为
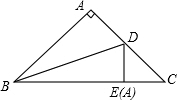 如图,等腰直角△ABC中,∠A=90°,AB=AC,把等腰直角△ABC沿BD折叠,使点A落在边BC上的点E处,CE=1,求BC的长.
如图,等腰直角△ABC中,∠A=90°,AB=AC,把等腰直角△ABC沿BD折叠,使点A落在边BC上的点E处,CE=1,求BC的长.