题目内容
2.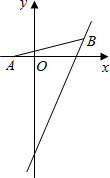 如图,点A的坐标为(-1,0),点B在直线y=2x-4上运动,当线段AB最短时,求点B的坐标.
如图,点A的坐标为(-1,0),点B在直线y=2x-4上运动,当线段AB最短时,求点B的坐标.
分析 作AB′⊥BB′,B′即为当线段AB最短时B点坐标,求出AB′的解析式,与BB′组成方程组,求出其交点坐标即可.
解答 解:如图,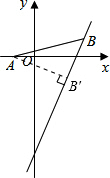
作AB′⊥BB′,
设AB′解析式为y=kx+b,
∵AB′⊥BB′,BB′解析式为y=2x-4,k1×k2=-1,
∴2k=-1,
k=-$\frac{1}{2}$,于是函数解析式为y=-$\frac{1}{2}$x+b,
将A(-1,0)代入y=-$\frac{1}{2}$x+b得,$\frac{1}{2}$+b=0,b=-$\frac{1}{2}$,
则函数解析式为y=-$\frac{1}{2}$x-$\frac{1}{2}$,
将两函数解析式组成方程组得,
$\left\{\begin{array}{l}{y=2x-4}\\{y=-\frac{1}{2}x-\frac{1}{2}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{7}{5}}\\{y=-\frac{6}{5}}\end{array}\right.$,
故B点坐标为($\frac{7}{5}$,-$\frac{6}{5}$).
点评 本题考查了一次函数的性质和垂线段最短,找到B′点是解题的关键,同时要熟悉待定系数法求函数解析式.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案
相关题目
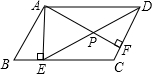 如图,在?ABCD中,AE⊥BC,AF⊥CD,∠EAF=60°,BE=3,CF=1.5,求AB,AF,DE的长.
如图,在?ABCD中,AE⊥BC,AF⊥CD,∠EAF=60°,BE=3,CF=1.5,求AB,AF,DE的长. 如图,在?ABCD中,已知AD=8cm,AB=6cm,DE平分∠ADC交BC边于点E,求BE的长.
如图,在?ABCD中,已知AD=8cm,AB=6cm,DE平分∠ADC交BC边于点E,求BE的长.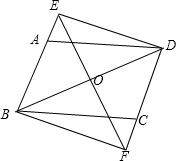 如图,点O为平行四边形ABCD的对角线BD的中点,直线EF经过点O,分别交BA,DC的延长线于E、F,求证:四边形BFDE是平行四边形.
如图,点O为平行四边形ABCD的对角线BD的中点,直线EF经过点O,分别交BA,DC的延长线于E、F,求证:四边形BFDE是平行四边形. 如图,在等腰△ABC中,过点A作CB的高,交CB的延长线于点D,若AB=2,∠ABC=120°,求sinC-tanC的值.
如图,在等腰△ABC中,过点A作CB的高,交CB的延长线于点D,若AB=2,∠ABC=120°,求sinC-tanC的值. 如图,B是AC边上一点,AD∥BE,∠1=∠2,求证:∠A=∠E.
如图,B是AC边上一点,AD∥BE,∠1=∠2,求证:∠A=∠E.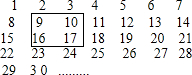 把连续的正整数1,2,3,4,…,按如图方式列成一个数表.
把连续的正整数1,2,3,4,…,按如图方式列成一个数表.