题目内容
12.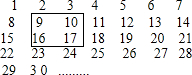 把连续的正整数1,2,3,4,…,按如图方式列成一个数表.
把连续的正整数1,2,3,4,…,按如图方式列成一个数表.(1)用一正方形框,按如图方式在表中任意框住4个数,记左上角的一个数为x,则这4个数的和是4x+16.(用含x的代数式表示).
(2)当(1)中被框住的4个数之和等于244时,x的值为多少?
(3)在(1)中能否框住这样的4个数,它们的和等于380?若能,则求出x的值;若不能,则说明理由.
分析 (1)左右相邻两个数差1,上下相邻的两个数相差为7,据此表示其它三个数,再相加即可求解;
(2)根据题意列出x+x+1+x+7+x+8=244,解一元一次方程求出x的值;
(3)令x+x+1+x+7+x+8=380,求出x的值,进而作出判断.
解答 解:(1)由图表可知:左右相邻两个数差1,上下相邻的两个数相差为7,左上角的一个数为x,
则另外三个数用含x的式子从小到大依次表示x+1;x+7;x+8,
x+x+1+x+7+x+8=4x+16.
故答案为:4x+16;
(2)根据题意可得:
x+x+1+x+7+x+8=244,
4x+16=244,
解得x=57.
答:x的值为57;
(3)假设x+x+1+x+7+x+8=380,
解得x=91.
因为91是第13行最后1个数,
所以它们不可能被(1)中的正方形框框住.
点评 本题主要考查了一元一次方程组的应用,解答本题的关键是掌握上下每列两个数相差为7,此题难度不大.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
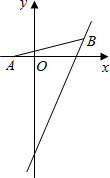 如图,点A的坐标为(-1,0),点B在直线y=2x-4上运动,当线段AB最短时,求点B的坐标.
如图,点A的坐标为(-1,0),点B在直线y=2x-4上运动,当线段AB最短时,求点B的坐标.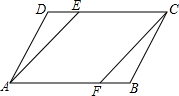 如图,在平行四边形ABCD中,BF=DE,求证:∠BAE=∠DCF.
如图,在平行四边形ABCD中,BF=DE,求证:∠BAE=∠DCF. 小明和小华在一栋大楼的前面估计楼房高度.小明说这楼有20层!小华说没有20层.为了验证他们的观点,他们在大楼两侧选择A、B两个点,经过测量AB=150米,CD=10米.∠A=30°,∠B=45°.不计两个人的身高,且A、B、C、D四个点在同一直线上.
小明和小华在一栋大楼的前面估计楼房高度.小明说这楼有20层!小华说没有20层.为了验证他们的观点,他们在大楼两侧选择A、B两个点,经过测量AB=150米,CD=10米.∠A=30°,∠B=45°.不计两个人的身高,且A、B、C、D四个点在同一直线上. 如图,从A路口到B路口有①、②、③三条路线可走,人们一般情况下选择走②号路线,用几何知识解释其道理应是两点之间,线段最短.
如图,从A路口到B路口有①、②、③三条路线可走,人们一般情况下选择走②号路线,用几何知识解释其道理应是两点之间,线段最短. 已知抛物线y1=x2+4x+1的图象向上平移m个单位(m>0)得到的新抛物线过点(1,8).
已知抛物线y1=x2+4x+1的图象向上平移m个单位(m>0)得到的新抛物线过点(1,8).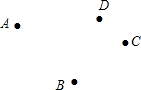 已知平面上A、B、C、D四个点,请用直尺按下列步骤要求完成画图.
已知平面上A、B、C、D四个点,请用直尺按下列步骤要求完成画图.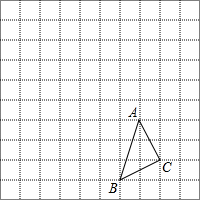 △ABC在方格中的位置如图所示.
△ABC在方格中的位置如图所示.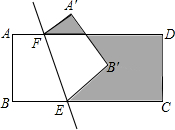 如图,矩形ABCD中,AB=2cm,BC=5cm,将四边形ABEF沿直线EF折叠,点A落在A′处,点B落在B′处,则阴影部分的周长为14cm.
如图,矩形ABCD中,AB=2cm,BC=5cm,将四边形ABEF沿直线EF折叠,点A落在A′处,点B落在B′处,则阴影部分的周长为14cm.