题目内容
12.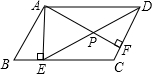 如图,在?ABCD中,AE⊥BC,AF⊥CD,∠EAF=60°,BE=3,CF=1.5,求AB,AF,DE的长.
如图,在?ABCD中,AE⊥BC,AF⊥CD,∠EAF=60°,BE=3,CF=1.5,求AB,AF,DE的长.
分析 由四边形内角和为360°,可先求∠C,再求∠ADC,∠B.分别在两个直角三角形中,解直角三角形即可求出AB,AF,DE的长.
解答 解:∵AE⊥BC,AF⊥CD,
∴∠AEC=∠AFC=90°,
∵∠EAF=60°,∠C+∠AEC+∠AFC+∠EAF=360°,
∴∠C+90°+90°+60°=360°,
∴∠C=120°,
∴∠ADC=∠B=60°,
∵BE=3,
∴AB=2BE=6,
∵CF=1.5,
∴DF=4.5,
∴AF=$\frac{9}{2}\sqrt{3}$,AD=9,
∵AE=3$\sqrt{3}$,AD=9,
∴DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=3$\sqrt{6}$.
点评 本题结合直角三角形考查了平行四边形的性质,平行四边形的性质有:(1)平行四边形的对边平行且相等.(2)平行四边形的对角相等;(3)平行四边形的对角线互相平分.

练习册系列答案
相关题目
3.某市中小学统一组织文艺演出活动,甲、乙两所学校共92人(其中甲校人数多于乙校人数,且甲校人数少于90人)准备统一购买服装参加演出,下面是某服装厂给出的演出服装的价格表:
如果两校分别单独购买服装,一共应付5000元.
(1)如果甲、乙两校联合起来购买服装,那么比各自购买服装共可以节省多少钱?
(2)甲、乙两校各有多少学生准备参加演出?
(3)如果甲校有8名同学抽调去参加汉字听写大会而不能参加演出,请为两校设计一种省钱的购买服装方案.
| 购买服装的套数 | 1套至45套 | 46套至90套 | 91套及以上 |
| 每套服装的价格 | 60元 | 50元 | 40元 |
(1)如果甲、乙两校联合起来购买服装,那么比各自购买服装共可以节省多少钱?
(2)甲、乙两校各有多少学生准备参加演出?
(3)如果甲校有8名同学抽调去参加汉字听写大会而不能参加演出,请为两校设计一种省钱的购买服装方案.
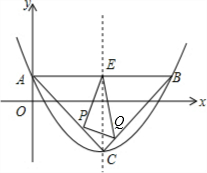 以C(4,-2)为顶点的抛物线交y轴于点A(0,1),过点A平行于x轴的直线交抛物线于点B,交抛物线对称轴于点E.
以C(4,-2)为顶点的抛物线交y轴于点A(0,1),过点A平行于x轴的直线交抛物线于点B,交抛物线对称轴于点E.
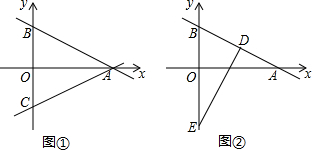
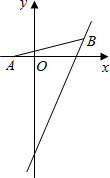 如图,点A的坐标为(-1,0),点B在直线y=2x-4上运动,当线段AB最短时,求点B的坐标.
如图,点A的坐标为(-1,0),点B在直线y=2x-4上运动,当线段AB最短时,求点B的坐标.