题目内容
7.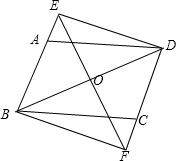 如图,点O为平行四边形ABCD的对角线BD的中点,直线EF经过点O,分别交BA,DC的延长线于E、F,求证:四边形BFDE是平行四边形.
如图,点O为平行四边形ABCD的对角线BD的中点,直线EF经过点O,分别交BA,DC的延长线于E、F,求证:四边形BFDE是平行四边形.
分析 连接AC,根据平行四边形的性质,可得AB与DC的关系,AO与OC的关系,根据全等三角形的性质,可得AE与CF的关系,根据平行四边形的判定,可得答案.
解答 证明:连接AC,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,OA=OC,
∴∠OEA=∠OFC.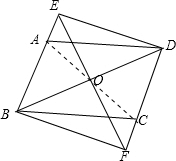
在△OAE和△OCF中,
$\left\{\begin{array}{l}{∠OEA=∠OFC}\\{∠AOE=∠COF}\\{OA=OC}\end{array}\right.$,
∴△OAE≌△OCF (AAS),
∴AE=CF,
∴AE+AB=CF+CD,
即BE=DF,
又∵BE∥DF,
∴四边形BFDE是平行四边形.
点评 本题考查了平行四边形的判定与性质以及全等三角形的判定和性质,掌握平行四边形的判定方法,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法是解题关键.

练习册系列答案
相关题目
 如图△ABC,用直尺和圆规按要求作图(不写作法,保留作图痕迹)
如图△ABC,用直尺和圆规按要求作图(不写作法,保留作图痕迹)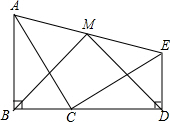 如图,△ABC≌△CDE,B、C、D三点共线,连接AE,点M为AE中点,连接BM、DM,试判断△BMD的形状.
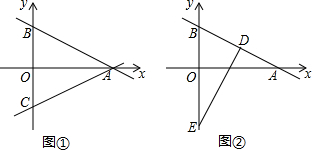
如图,△ABC≌△CDE,B、C、D三点共线,连接AE,点M为AE中点,连接BM、DM,试判断△BMD的形状.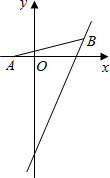 如图,点A的坐标为(-1,0),点B在直线y=2x-4上运动,当线段AB最短时,求点B的坐标.
如图,点A的坐标为(-1,0),点B在直线y=2x-4上运动,当线段AB最短时,求点B的坐标.
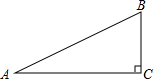 如图,在Rt△ABC中,∠A=30°,
如图,在Rt△ABC中,∠A=30°, 已知抛物线y1=x2+4x+1的图象向上平移m个单位(m>0)得到的新抛物线过点(1,8).
已知抛物线y1=x2+4x+1的图象向上平移m个单位(m>0)得到的新抛物线过点(1,8).