题目内容
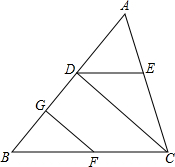 如图,已知点D、G、E、F分别是三角形ABC的边AB、AC、BC上的点,CD⊥AB于点D,∠B=∠ADE,∠EDC=∠GFB.
如图,已知点D、G、E、F分别是三角形ABC的边AB、AC、BC上的点,CD⊥AB于点D,∠B=∠ADE,∠EDC=∠GFB.求证:FG⊥AB.
考点:平行线的判定与性质
专题:证明题
分析:根据∠B=∠ADE得出∠EDC=∠DCF,再根据∠EDC=∠GFB,得出GF∥CD,最后根据CD⊥AB,即可证出FG⊥AB.
解答:证明:∵∠B=∠ADE,
∴DE∥BC,
∴∠EDC=∠DCF,
∵∠EDC=∠GFB,
∴∠DCF=∠GFB,
∴GF∥CD,
∵CD⊥AB,
∴∠CDG=∠FGB=90°,
∴FG⊥AB.
∴DE∥BC,
∴∠EDC=∠DCF,
∵∠EDC=∠GFB,
∴∠DCF=∠GFB,
∴GF∥CD,
∵CD⊥AB,
∴∠CDG=∠FGB=90°,
∴FG⊥AB.
点评:本题考查了平行线性质和判定,主要考查了学生的推理能力,解答此题的关键是注意平行线的性质和判定定理的综合运用.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
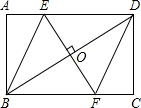 如图,矩形ABCD,过对角线BD的中点O作BD的垂线交AD于E,交BC于F,连结EB、DF.
如图,矩形ABCD,过对角线BD的中点O作BD的垂线交AD于E,交BC于F,连结EB、DF. 如图,如果△AOB的周长比△AOD的周长大5,并且AB:AD=3:2,那么?ABCD的周长为多少?
如图,如果△AOB的周长比△AOD的周长大5,并且AB:AD=3:2,那么?ABCD的周长为多少?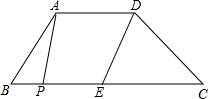 如图,在梯形ABCD中,AD∥BC,E是BC的中点,AD=5,BC=12,CD=4
如图,在梯形ABCD中,AD∥BC,E是BC的中点,AD=5,BC=12,CD=4