题目内容
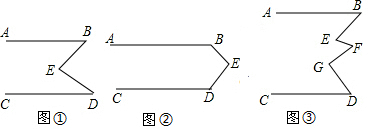
10.(1)如图①,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?(2)反之,在图①中,若∠B+∠D=∠E,直线AB与CD有什么位置关系?
(3)若将点E移至图②的位置,此时∠B,∠D,∠E之间有什么关系?
(4)在图③中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?
分析 (1)首先作EF∥AB,根据AB∥CD,可得EF∥CD,据此分别判断出∠B=∠1,∠D=∠2,即可判断出∠B+∠D=∠E,据此解答即可.
(2)首先作EF∥AB,即可判断出∠B=∠1;然后根据∠E=∠1+∠2=∠B+∠D,可得∠D=∠2,据此判断出EF∥CD,再根据EF∥AB,可得AB∥CD,据此判断即可.
(3)首先过E作EF∥AB,即可判断出∠BEF+∠B=180°,然后根据EF∥CD,可得∠D+∠DEF=180°,据此判断出∠E+∠B+∠D=360°即可.
(4)首先作EM∥AB,FN∥AB,GP∥AB,根据AB∥CD,可得∠B=∠1,∠2=∠3,∠4=∠5,∠6=∠D,所以∠1+∠2+∠5+∠6=∠B+∠3+∠4+∠D;然后根据∠1+∠2=∠E,∠5+∠6=∠G,∠3+∠4=∠F,可得∠E+∠G=∠B+∠F+∠D,据此判断即可.
解答  解:(1)如图1,作EF∥AB,
解:(1)如图1,作EF∥AB,
∵AB∥CD,
∴∠B=∠1,
∵AB∥CD,EF∥AB,
∴EF∥CD,
∴∠D=∠2,
∴∠B+∠D=∠1+∠2,
又∵∠1+∠2=∠E,
∴∠B+∠D=∠E.
(2)如图2,作EF∥AB,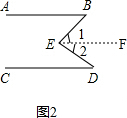
∵EF∥AB,
∴∠B=∠1,
∵∠BED=∠1+∠2=∠B+∠D,
∴∠D=∠2,
∴EF∥CD,
又∵EF∥AB,
∴AB∥CD.
(3)如图3,过E作EF∥AB,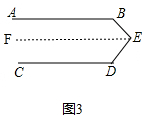
∵EF∥AB,
∴∠BEF+∠B=180°,
∵EF∥CD,
∴∠D+∠DEF=180°,
∵∠BEF+∠DEF=∠E,
∴∠E+∠B+∠D=180°+180°=360°.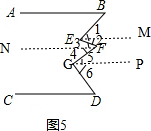
(4)如图5,作EM∥AB,FN∥AB,GP∥AB,
∵AB∥CD,
∴∠B=∠1,∠2=∠3,∠4=∠5,∠6=∠D,
∴∠1+∠2+∠5+∠6=∠B+∠3+∠4+∠D;
∵∠1+∠2=∠E,∠5+∠6=∠G,∠3+∠4=∠F,
∴∠E+∠G=∠B+∠F+∠D.
点评 此题主要考查了平行线的性质,解答此题的关键是要明确:两条平行线被第三条直线所截,同旁内角互补;两条平行线被第三条直线所截,内错角相等.

 如图,已知直线a、b被直线c所截,那么∠1的同位角是( )
如图,已知直线a、b被直线c所截,那么∠1的同位角是( )| A. | ∠2 | B. | ∠3 | C. | ∠4 | D. | ∠5 |
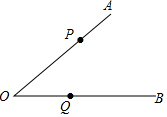 已知点P、Q分别在∠ACB的边OA、OB上,按下列要求画图
已知点P、Q分别在∠ACB的边OA、OB上,按下列要求画图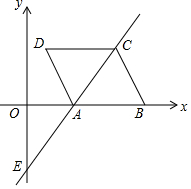 已知:菱形ABCD在直角坐标系中的位置如图所示,与y轴交与点E的直线y=$\frac{3}{2}$x-3过点A和点C,且点A平分线段CE.
已知:菱形ABCD在直角坐标系中的位置如图所示,与y轴交与点E的直线y=$\frac{3}{2}$x-3过点A和点C,且点A平分线段CE.