题目内容
1.计算:(1)$\sqrt{48}$+$\sqrt{3}$-$\sqrt{\frac{1}{2}}$×$\sqrt{12}$+$\sqrt{24}$
(2)($\sqrt{2}$+$\sqrt{3}$)2(5-2$\sqrt{6}$)
(3)(2$\sqrt{48}$-3$\sqrt{27}$)÷$\sqrt{6}$
(4)($\sqrt{48}$-4$\sqrt{\frac{1}{8}}$)-(3$\sqrt{\frac{1}{3}}$-2$\sqrt{0.5}$)
分析 (1)先进行二次根式的乘法运算,然后把各二次根式化简为最简二次根式后合并即可;
(2)先利用完全平方公式计算,然后利用平方差公式计算;
(3)把括号内的各二次根式化简为最简二次根式,然后合并后进行二次根式的除法运算;
(4)先把各二次根式化简为最简二次根式,然后去括号后合并即可.
解答 解:(1)原式=4$\sqrt{3}$+$\sqrt{3}$-$\sqrt{\frac{1}{2}×12}$+2$\sqrt{6}$
=5$\sqrt{3}$-$\sqrt{6}$+2$\sqrt{6}$
=5$\sqrt{3}$+$\sqrt{6}$;
(2)原式=(5+2$\sqrt{6}$)(5-2$\sqrt{6}$)
=25-24
=1;
(3)原式=(8$\sqrt{3}$-9$\sqrt{3}$)÷$\sqrt{6}$
=-$\sqrt{3}$÷$\sqrt{6}$
=-$\frac{\sqrt{2}}{2}$;
(4)原式=4$\sqrt{3}$-$\sqrt{2}$-$\sqrt{3}$+$\sqrt{2}$
=3$\sqrt{3}$.
点评 本题考查了二次根式的混合运算:先把各二次根式化简为最简二次根式,然后进行二次根式的乘除运算,再合并即可.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 如图,正方形ABCD中,E为BC中点,DF=$\frac{1}{2}$CF
如图,正方形ABCD中,E为BC中点,DF=$\frac{1}{2}$CF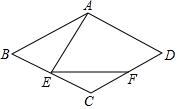 如图,四边形ABCD为菱形,∠C=120°,点E是BC上一点.∠AEF=60°,EF交CD于F,求证:(1)∠BAE=∠CEF;(2)AE=EF.
如图,四边形ABCD为菱形,∠C=120°,点E是BC上一点.∠AEF=60°,EF交CD于F,求证:(1)∠BAE=∠CEF;(2)AE=EF.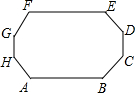 如图,凸八边形ABCDEFGH的8个内角都相等,边AB、BC、CD、DE、EF、FG的长分别为7,4,2,5,6,2,求该八边形的周长.
如图,凸八边形ABCDEFGH的8个内角都相等,边AB、BC、CD、DE、EF、FG的长分别为7,4,2,5,6,2,求该八边形的周长.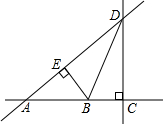 如图所示,直线AD与直线BD相交于点D,BE⊥AD垂足为点E,点B到直线AD的距离是线段BE的长度,点D到直线AB的距离是线段DC的长度.
如图所示,直线AD与直线BD相交于点D,BE⊥AD垂足为点E,点B到直线AD的距离是线段BE的长度,点D到直线AB的距离是线段DC的长度.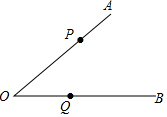 已知点P、Q分别在∠ACB的边OA、OB上,按下列要求画图
已知点P、Q分别在∠ACB的边OA、OB上,按下列要求画图