题目内容
9.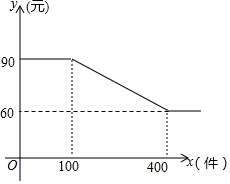 某衬衫厂生产某品牌衬衫的成本价为50元/件,批发价y元/件与一次性批发件数x件之间的关系满足图中折线的函数关系,批发件数为10的正整数倍.
某衬衫厂生产某品牌衬衫的成本价为50元/件,批发价y元/件与一次性批发件数x件之间的关系满足图中折线的函数关系,批发件数为10的正整数倍.(1)直接写出y与x的函数关系式,并写出自变量的取值范围;
(2)若某商户一次批发件数不超过400件,求此商户一次批发多少件时,衬衫厂获利最大?最大利润是多少?
分析 (1)根据函数图象和函数图象中的数据可以求得各段对应的函数解析式和自变量的取值范围;
(2)根据题意和分类讨论的数学思想可以求得一次批发件数不超过400件时的最大利润.
解答 解:(1)当10≤x≤100且x为10的正整数倍时,y=90,
当100<x≤400且x为10的正整数倍时,设y=kx+b,
$\left\{\begin{array}{l}{100k+b=90}\\{400k+b=60}\end{array}\right.$,得$\left\{\begin{array}{l}{k=-\frac{1}{10}}\\{b=100}\end{array}\right.$,
即当100<x≤400且x为10的正整数倍时,y=$-\frac{1}{10}x+100$,
当x>400且x为10的正整数倍时,y=60;
(2)设衬衫厂获利为w元,
当10≤x≤100且x为10的正整数倍时,w=(90-50)x=40x,
∴当x=100时,w取得最大值,此时w=4000,
当100<x≤400且x为10的正整数倍时,w=x(y-50)=x($-\frac{1}{10}x+100$-50)=$-\frac{1}{10}(x-250)^{2}+6250$,
∴当x=250时,w取得最大值,此时w=6250,
由上可得,若某商户一次批发件数不超过400件,此商户一次批发250件时,衬衫厂获利最大,最大利润是6250元.
点评 本题考查二次函数的应用,解答本题的关键是明确题意,利用分类讨论的数学思想和二次函数的性质解答问题.

练习册系列答案
相关题目
18.某市中学组织学生到距离学校6km的神舟科技馆去参观,学生李伟因事故耽误没能乘上学校的专车,于是准备在学校门口改乘出租车去神舟科技馆,出租车的收费标准如下:
(1)写出出租车行驶的里程数x(x≥2km)与费用y(元)之间的函数关系式;
(2)李伟同学身上仅有16元钱,乘出租车到科技馆的车费够不够?请说明理由.
| 里程 | 收费 |
| 2km以内(含2km) | 10.0 |
| 2km以上,每增加1km | 1.40 |
(2)李伟同学身上仅有16元钱,乘出租车到科技馆的车费够不够?请说明理由.
19.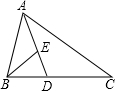 如图,△ABC中,D、E两点分别在BC、AD上,且AD平分∠BAC,若∠ABE=∠C,AD:ED=3:1,则△BDE与△ADC的面积比为( )
如图,△ABC中,D、E两点分别在BC、AD上,且AD平分∠BAC,若∠ABE=∠C,AD:ED=3:1,则△BDE与△ADC的面积比为( )
 如图,△ABC中,D、E两点分别在BC、AD上,且AD平分∠BAC,若∠ABE=∠C,AD:ED=3:1,则△BDE与△ADC的面积比为( )
如图,△ABC中,D、E两点分别在BC、AD上,且AD平分∠BAC,若∠ABE=∠C,AD:ED=3:1,则△BDE与△ADC的面积比为( )| A. | 16:45 | B. | 2:9 | C. | 1:9 | D. | 1:3 |
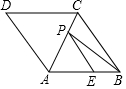 如图,菱形ABCD的边长为5,对角线AC=2$\sqrt{5}$,点E在边AB上,BE=2,点P是AC上的一个动点,则PB+PE的最小值为2$\sqrt{13}$.
如图,菱形ABCD的边长为5,对角线AC=2$\sqrt{5}$,点E在边AB上,BE=2,点P是AC上的一个动点,则PB+PE的最小值为2$\sqrt{13}$.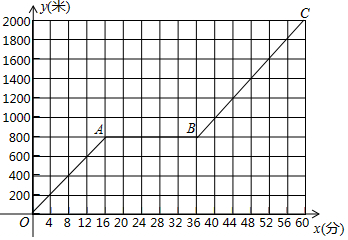 小明家到公园的路程为2000米,小明爸爸和小明先后从家出发步行去公园.爸爸先出发一直匀速前行,小明在爸爸走出200米后出发,途中他在休闲广场观棋停留一段时间.小明所走路程y(米)与步行时间x(分)的函数图象如图所所示.
小明家到公园的路程为2000米,小明爸爸和小明先后从家出发步行去公园.爸爸先出发一直匀速前行,小明在爸爸走出200米后出发,途中他在休闲广场观棋停留一段时间.小明所走路程y(米)与步行时间x(分)的函数图象如图所所示.
 已知:如图,在△ABC中,∠ABC=45°,tanA=$\frac{3}{4}$,AB=14,
已知:如图,在△ABC中,∠ABC=45°,tanA=$\frac{3}{4}$,AB=14,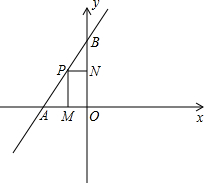 如图,在平面直角坐标系中,直线y=$\frac{3}{2}$x+6与x轴交于点A,与y轴交于点B,P为线段AB上一动点(不与A,B两点重合),过点P作PM⊥x轴,PN⊥y轴,垂足分别为M,N.设OM=a,四边形PMON面积为s.
如图,在平面直角坐标系中,直线y=$\frac{3}{2}$x+6与x轴交于点A,与y轴交于点B,P为线段AB上一动点(不与A,B两点重合),过点P作PM⊥x轴,PN⊥y轴,垂足分别为M,N.设OM=a,四边形PMON面积为s.