Question

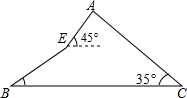如图所示，甲、乙两班学生进行爬山比赛，甲班学生从西坡沿坡角为30°的山坡爬了200米，紧接着又爬了坡角为45°的山坡80米，最后到达山顶；乙班学生从东坡沿着坡角为35°的斜坡爬向山顶，若两班学生爬山的平均速度相同，请问哪班学生先到达山顶．（结果精确到个位，参考数据：

2

≈1.4，

3

≈1.7，sin35°≈0.5736，cos35°≈.8192，tan35°≈0.7002）．

Answer 1

考点：解直角三角形的应用-坡度坡角问题

专题：

分析：作EF⊥BC于F，AK⊥EK于K交BC于T，则AT⊥BC．利用三角函数求出AC，比较BE+AE和AC的长即可．

解答：解：作EF⊥BC于F，AK⊥EK于K交BC于T，则AT⊥BC．
∵EF=BE•sin30°=200×

1

2

=100米，
AK=AE•sin45°=80×

2

2

=40

2

米，
∴AT=AK+EF=（40

2

+100）米．
在Rt△ATC中，

AT

AC

=sin35°，
AC=

AT

sin35°

≈

40 2 +100

0.5736

≈273米，
又∵BE+AE=200+80=280米，两班学生爬山的平均速度相同，
∴乙班学生先到山顶．

点评：本题考查了解直角三角形--坡度坡角问题，熟悉三角函数及坡角是解题的关键．