题目内容
已知∠α与∠β互为余角，且它们的度数之比为2：3，求∠β-∠α的度数．
考点：余角和补角
专题：
分析：设∠α=2x，∠β=3x，然后根据∠α与∠β互为余角，可列出方程：2x+3x=90°，解出x的值，从而确定∠α，∠β的值即可求解．
解答：解：设∠α=2x，∠β=3x，根据题意得：
2x+3x=90°，
解得：x=18°，
所以∠α=2x=36°，∠β=3x=54°，
所以∠β-∠α=54°-36°=18°．
所以∠β-∠α的度数为：18°．
2x+3x=90°，
解得：x=18°，
所以∠α=2x=36°，∠β=3x=54°，
所以∠β-∠α=54°-36°=18°．
所以∠β-∠α的度数为：18°．
点评：本题考查了余角和补角的知识，解答本题的关键是掌握互余两角之和为90°．
练习册系列答案
相关题目
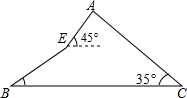如图所示，甲、乙两班学生进行爬山比赛，甲班学生从西坡沿坡角为30°的山坡爬了200米，紧接着又爬了坡角为45°的山坡80米，最后到达山顶；乙班学生从东坡沿着坡角为35°的斜坡爬向山顶，若两班学生爬山的平均速度相同，请问哪班学生先到达山顶．（结果精确到个位，参考数据：同一坐标系中，抛物线y=（x-a）2与直线y=a+ax的图象可能是（ ）
A、 |
B、 |
C、 |
D、 |
若y=（m2+3m+2）xm2+m为二次函数，则m的值为（ ）
| A、-2 或1 | B、-2 |
| C、-1 | D、1 |