题目内容
19.已知二次函数y=a(x2-4x-5),a≠0,下列说法:①图象始终与x轴有两个交点;
②图象的对称轴是直线x=2;
③图象在x轴上截得的线段长为6;
④若a<0,则当-1<x<5时,y>0;
其中,正确的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 将y=0代入y=a(x2-4x-5)(a≠0),解方程a(x2-4x-5)=0,求出x1=-1,x2=5,即可判断①;
根据二次函数y=ax2+bx+c(a≠0)的对称轴直线x=-$\frac{b}{2a}$即可判断②;
由二次函数y=a(x2-4x-5)与x轴交点为(-1,0),(5,0),求出图象在x轴上截得的线段长,即可判断③;
由a<0,得出抛物线y=a(x2-4x-5)开口向下,根据二次函数的性质可知当-1<x<5时,y>0,即可判断④.
解答 解:①∵y=a(x2-4x-5),a≠0,
∴当y=0时,a(x2-4x-5)=0,
解得x1=-1,x2=5,
∴图象始终与x轴有两个交点,故说法正确;
②图象的对称轴是直线x=$\frac{4a}{2a}$=2,故说法正确;
③∵二次函数y=a(x2-4x-5)与x轴交点为(-1,0),(5,0),
∴图象在x轴上截得的线段长为:5-(-1)=6,故说法正确;
④若a<0,则抛物线y=a(x2-4x-5)开口向下,
∴当-1<x<5时,y>0,故说法正确;
所以正确的命题为①②③④.
故选D.
点评 本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),对称轴是直线x=-$\frac{b}{2a}$.当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-$\frac{b}{2a}$时,y随x的增大而减小;x>-$\frac{b}{2a}$时,y随x的增大而增大;x=-$\frac{b}{2a}$时,y取得最小值$\frac{4ac-{b}^{2}}{4a}$,即顶点是抛物线的最低点.当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-$\frac{b}{2a}$时,y随x的增大而增大;x>-$\frac{b}{2a}$时,y随x的增大而减小;x=-$\frac{b}{2a}$时,y取得最大值$\frac{4ac-{b}^{2}}{4a}$,即顶点是抛物线的最高点.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案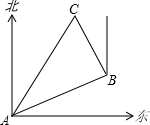 如图,在一次夏令营活动中,小明从营地A到C地去,先沿北偏东70°方向到达B地,再沿北偏西20°方向到达C地,此时∠ACB=60°,问小明在营地A的( )
如图,在一次夏令营活动中,小明从营地A到C地去,先沿北偏东70°方向到达B地,再沿北偏西20°方向到达C地,此时∠ACB=60°,问小明在营地A的( )| A. | 北偏东20°方向上 | B. | 北偏东30°方向上 | C. | 北偏西30°方向上 | D. | 北偏东40°方向上 |
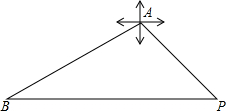 北京时间2014年3月8日凌晨1时20分,由马来西亚飞往北京的马来西亚航空公司MH370航班于地面失去联系,机上239人中包括153名中国大陆乘客.飞机可能出事的海域在点P的正西方向且距离P约2000海里的点B处,中国海上搜救中心的海警船3411在点A观测P点在东偏南45度方向,观测飞机疑似“终结”区域点B在点A的西偏南30度方向,海警船点A到疑似出事区域点B的距离.
北京时间2014年3月8日凌晨1时20分,由马来西亚飞往北京的马来西亚航空公司MH370航班于地面失去联系,机上239人中包括153名中国大陆乘客.飞机可能出事的海域在点P的正西方向且距离P约2000海里的点B处,中国海上搜救中心的海警船3411在点A观测P点在东偏南45度方向,观测飞机疑似“终结”区域点B在点A的西偏南30度方向,海警船点A到疑似出事区域点B的距离.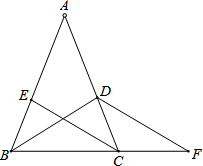 如图:∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,∠DBF=∠F,那么EC与DF平行吗?为什么?请完成下面的解题过程.
如图:∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,∠DBF=∠F,那么EC与DF平行吗?为什么?请完成下面的解题过程.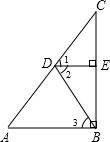 如图,∠1=∠2,DE⊥BC,AB⊥BC,那么∠A=∠3吗?说明理由.(请为每一步推理注明依据)
如图,∠1=∠2,DE⊥BC,AB⊥BC,那么∠A=∠3吗?说明理由.(请为每一步推理注明依据)