题目内容
下列不等关系一定正确的是( )
A.|a|>0 B.﹣x2<0 C.(x+1)2≥0 D.a2>0
 C
【解析】
试题分析:根据绝对值及完全平方式的性质求解.
【解析】
A、|a|≥0,错误;
B、﹣x2≤0,错误;
C、(x+1)2≥0,正确;
D、a2≥0,错误,
故选C.
C
【解析】
试题分析:根据绝对值及完全平方式的性质求解.
【解析】
A、|a|≥0,错误;
B、﹣x2≤0,错误;
C、(x+1)2≥0,正确;
D、a2≥0,错误,
故选C.
 计算高手系列答案
计算高手系列答案化简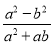 的结果为( )
的结果为( )
A. 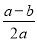 B.
B. 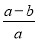 C.
C. 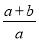 D.
D. 
 B
【解析】=,故选B.
B
【解析】=,故选B. 如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.
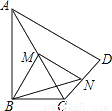
 (1)证明见解析;(2)
【解析】试题分析:(1)在△CAD中,由中位线定理得到MN∥AD,且MN=AD,在Rt△ABC中,因为M是AC的中点,故BM=AC,即可得到结论;
(2)由∠BAD=60°且AC平分∠BAD,得到∠BAC=∠DAC=30°,由(1)知,BM=AC=AM=MC,得到∠BMC =60°.由平行线性质得到∠NMC=∠DAC=30°,故∠BMN90°,得到,再由MN=...
(1)证明见解析;(2)
【解析】试题分析:(1)在△CAD中,由中位线定理得到MN∥AD,且MN=AD,在Rt△ABC中,因为M是AC的中点,故BM=AC,即可得到结论;
(2)由∠BAD=60°且AC平分∠BAD,得到∠BAC=∠DAC=30°,由(1)知,BM=AC=AM=MC,得到∠BMC =60°.由平行线性质得到∠NMC=∠DAC=30°,故∠BMN90°,得到,再由MN=... 有一个两位数,个位上的数字为a,十位上的数字为b,如果把这个两位数的个位与十位上的数字对调,得到的两位数大于原来的两位数,那么a与b哪个大?
 a>b
【解析】试题分析:根据题意得到不等式10b+a<10a+b,通过解该不等式即可比较它们的大小.
试题解析:根据题意,得
10b+a<10a+b,
所以,9b<9a,
所以,b<a,即a>b.
a>b
【解析】试题分析:根据题意得到不等式10b+a<10a+b,通过解该不等式即可比较它们的大小.
试题解析:根据题意,得
10b+a<10a+b,
所以,9b<9a,
所以,b<a,即a>b. 一所中学的男子百米赛跑的记录是11.7秒,假设一名男运动员的百米赛跑成绩为x秒,如果这名运动员破记录,则__________;如果这名运动员没破记录,则________.
 x<11.7, x≥11.7
【解析】由题意得:∵百米赛跑的记录是11.7秒,
∴要破纪录则x<ll.7,
没破纪录x≥11.7,
故答案为:x<11.7,x≥11.7.
x<11.7, x≥11.7
【解析】由题意得:∵百米赛跑的记录是11.7秒,
∴要破纪录则x<ll.7,
没破纪录x≥11.7,
故答案为:x<11.7,x≥11.7. 将△ABC的∠C折起,翻折后角的顶点位置记作C′,当C′落在AC上时(如图1),易证:∠1=2∠2.
当C′点落在CA和CB之间(如图2)时,或当C′落在CB、CA的同旁(如图3)时,∠1、∠2、∠3关系又如何?请写出你的猜想,并就其中一种情况给出证明.
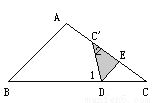


图1 图2 图3
 见解析
【解析】利用轴对称的知识找出等解即可进行推理判断.
【解析】
当C′点落在CA和CB之间(如图2)时,∠1+∠3=2∠2;
当C′落在CB、CA的同旁(如图3)时,∠1-∠3=2∠2;
对于图2证明如下:
连结CC’,如图4所示,
∵⊿EC’D是由⊿ECD翻折得到的,
∴⊿EC’D≌⊿ECD,由此得EC=EC’,DC=DC’,∠EC’D=∠ECD...
见解析
【解析】利用轴对称的知识找出等解即可进行推理判断.
【解析】
当C′点落在CA和CB之间(如图2)时,∠1+∠3=2∠2;
当C′落在CB、CA的同旁(如图3)时,∠1-∠3=2∠2;
对于图2证明如下:
连结CC’,如图4所示,
∵⊿EC’D是由⊿ECD翻折得到的,
∴⊿EC’D≌⊿ECD,由此得EC=EC’,DC=DC’,∠EC’D=∠ECD... 如图,矩形ABCD中将其沿EF翻折后,D点恰落在B处,∠BFE= 650,则∠AEB=____________.
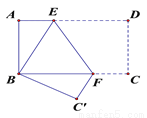
 50°
【解析】根据翻折求出各个角的度数,再根据平角180°求出∠AEB的度数即可.
【解析】
如图所示,
由矩形ABCD可得AD∥BC,
∴∠1=∠BFE =65°,
由翻折得∠2=∠1 =65°,
∴∠AEB =180°-∠1- ∠2 =180°-65°-65°=50°.
50°
【解析】根据翻折求出各个角的度数,再根据平角180°求出∠AEB的度数即可.
【解析】
如图所示,
由矩形ABCD可得AD∥BC,
∴∠1=∠BFE =65°,
由翻折得∠2=∠1 =65°,
∴∠AEB =180°-∠1- ∠2 =180°-65°-65°=50°. 如图,A与A′关于直线MN对称,P是BA′与MN的交点.若P1为直线MN上任意一点(不与P重合),连结AP1、BP1,试说明 AP1+BP1>AP+BP.
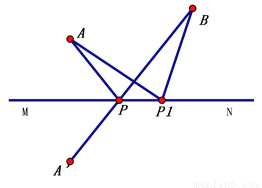
 见解析
【解析】试题分析:由三角形三条边的关系可得A′P1+BP1>A′B,再由轴对称的性质可得AP1=A′P1,然后通过等量代换可证明结论.
【解析】
如图,连结AP1,则在△A′P1B中,有A′P1+BP1>A′B
∴A′P1+BP1>A′P+PB
∵A与A′关于直线MN对称,
∴AP1与A′P1关于直线MN对称
∴AP1=A′P1
同理可得:AP=...
见解析
【解析】试题分析:由三角形三条边的关系可得A′P1+BP1>A′B,再由轴对称的性质可得AP1=A′P1,然后通过等量代换可证明结论.
【解析】
如图,连结AP1,则在△A′P1B中,有A′P1+BP1>A′B
∴A′P1+BP1>A′P+PB
∵A与A′关于直线MN对称,
∴AP1与A′P1关于直线MN对称
∴AP1=A′P1
同理可得:AP=... (吉安永新县期末)如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动.当四边形PQBC为平行四边形时,运动时间为( )
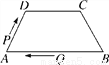
A. 4s B. 3s C. 2s D. 1s
 B
【解析】试题解析:设运动时间为t秒,则CP=12-3t,BQ=t,
根据题意得到12-3t=t,
解得:t=3,
故选B.
B
【解析】试题解析:设运动时间为t秒,则CP=12-3t,BQ=t,
根据题意得到12-3t=t,
解得:t=3,
故选B. 
