题目内容
7. 若把一组邻边的平方和与一条对角线的平方相等的四边形叫做勾股四边形,则矩形、直角梯形都是勾股四边形.如图,将△ABC绕点B顺时针旋转60°得到△DBE,且∠BCD=30°.
若把一组邻边的平方和与一条对角线的平方相等的四边形叫做勾股四边形,则矩形、直角梯形都是勾股四边形.如图,将△ABC绕点B顺时针旋转60°得到△DBE,且∠BCD=30°.(1)求证:四边形ABCD是勾股四边形;
(2)若BC=6,CD=8,求DE的长.
分析 (1)欲证明DC2+BC2=AC2,只需证明∠DCE=90°.
(2)由DC2+BC2=AC2,求出AC,即可得出DE的长.
解答 (1)证明:由旋转的性质得:△ABC≌△DBE,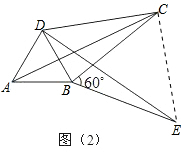
∴AC=DE,BC=BE,
∵∠CBE=60°,
∴EC=BC=BE,即△BCE是等边三角形,
∴∠BCE=60°,
∵∠DCB=30°,
∴∠DCE=90°,
∴DC2+EC2=DE2,
∴DC2+BC2=AC2.
即四边形ABCD是勾股四边形.
(2)解:由(1)得:DC2+BC2=AC2,DE=AC,
∴DE=AC=$\sqrt{{8}^{2}+{6}^{2}}$=10.
点评 本题考查了勾股定理、旋转的性质、全等三角形的性质、等边三角形的判定与性质、勾股定理;熟练掌握旋转的性质,证明∠DCE=90°是解决问题的关键.

练习册系列答案
相关题目
17. 如图,长方形ABCD中有6个形状、大小相同的小长方形,且EF=3,CD=12,则图中阴影部分的面积为( )
如图,长方形ABCD中有6个形状、大小相同的小长方形,且EF=3,CD=12,则图中阴影部分的面积为( )
 如图,长方形ABCD中有6个形状、大小相同的小长方形,且EF=3,CD=12,则图中阴影部分的面积为( )
如图,长方形ABCD中有6个形状、大小相同的小长方形,且EF=3,CD=12,则图中阴影部分的面积为( )| A. | 108 | B. | 72 | C. | 60 | D. | 48 |
18.下列命题中,是真命题的是( )
| A. | 对角线互相垂直的平行四边形是正方形 | |
| B. | 相似三角形的周长之比等于相似的平方 | |
| C. | 若(1,y1)、(2,y2)是双曲线y=-$\frac{1}{x}$上的两点,则y1<y2 | |
| D. | 方程x2-2x+3=0有两个不相等的实数根 |
15. 如图,A、D是电线杆AB上的两个瓷壶,AC和DE分别表示太阳光线,若某一时刻线段AD在地面上的影长CE=1m,BD在地面上的影长BE=3m,瓷壶D到地面的距离DB=20m,则电线杆AB的高为( )
如图,A、D是电线杆AB上的两个瓷壶,AC和DE分别表示太阳光线,若某一时刻线段AD在地面上的影长CE=1m,BD在地面上的影长BE=3m,瓷壶D到地面的距离DB=20m,则电线杆AB的高为( )
 如图,A、D是电线杆AB上的两个瓷壶,AC和DE分别表示太阳光线,若某一时刻线段AD在地面上的影长CE=1m,BD在地面上的影长BE=3m,瓷壶D到地面的距离DB=20m,则电线杆AB的高为( )
如图,A、D是电线杆AB上的两个瓷壶,AC和DE分别表示太阳光线,若某一时刻线段AD在地面上的影长CE=1m,BD在地面上的影长BE=3m,瓷壶D到地面的距离DB=20m,则电线杆AB的高为( )| A. | 15m | B. | $\frac{80}{3}$m | C. | 21m | D. | $\frac{60}{7}$m |
16.下列说法正确的是( )
| A. | 一个游戏的中奖概率是$\frac{1}{10}$,则做10次这样的游戏一定会中奖 | |
| B. | 为了解全国中学生的心理健康情况,适合采用抽样调查的方式 | |
| C. | 为了解某市九年级学生的肺活量,从中抽样调查了500名学生的肺活量,这项调查中的样本是从中抽取的500名学生 | |
| D. | 若甲组数据的方差S2=0.01,乙组数据的方差S2=0.1,则乙组数据比甲组数据稳定 |
 如图,某测量员测量公园内一棵树DE的高度,他们在这棵树左侧一斜坡上端点A处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为3米,台阶AC的坡度为1:$\sqrt{3}$(即AB:BC=1:$\sqrt{3}$),且B、C、E三点在同一条直线上.
如图,某测量员测量公园内一棵树DE的高度,他们在这棵树左侧一斜坡上端点A处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为3米,台阶AC的坡度为1:$\sqrt{3}$(即AB:BC=1:$\sqrt{3}$),且B、C、E三点在同一条直线上. 已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=$\sqrt{5}$,下列结论:①△APD≌△AEB;②点B到直线AE的距离为$\sqrt{2}$;③EB⊥ED;④S△APD+S△APB=$\frac{1+\sqrt{6}}{2}$.其中正确结论的序号是①③④.
已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=$\sqrt{5}$,下列结论:①△APD≌△AEB;②点B到直线AE的距离为$\sqrt{2}$;③EB⊥ED;④S△APD+S△APB=$\frac{1+\sqrt{6}}{2}$.其中正确结论的序号是①③④.