题目内容
2. 如图,某测量员测量公园内一棵树DE的高度,他们在这棵树左侧一斜坡上端点A处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为3米,台阶AC的坡度为1:$\sqrt{3}$(即AB:BC=1:$\sqrt{3}$),且B、C、E三点在同一条直线上.
如图,某测量员测量公园内一棵树DE的高度,他们在这棵树左侧一斜坡上端点A处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为3米,台阶AC的坡度为1:$\sqrt{3}$(即AB:BC=1:$\sqrt{3}$),且B、C、E三点在同一条直线上.(1)求斜坡AC的长;
(2)请根据以上条件求出树DE的高度(侧倾器的高度忽略不计).
分析 过点A作AF⊥DE于F,可得四边形ABEF为矩形,设DE=x,在Rt△DCE和Rt△ABC中分别表示出CE,BC的长度,求出DF的长度,然后在Rt△ADF中表示出AF的长度,根据AF=BE,代入解方程求出x的值即可.
解答 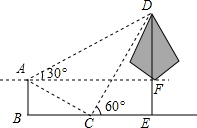 解:(1)如图,过点A作AF⊥DE于F,
解:(1)如图,过点A作AF⊥DE于F,
则四边形ABEF为矩形,
∴AF=BE,EF=AB=3米,
设DE=x,
在Rt△CDE中,CE=$\frac{DE}{tan60°}$=$\frac{\sqrt{3}}{3}$x,
在Rt△ABC中,
∵$\frac{AB}{BC}$=$\frac{1}{\sqrt{3}}$,AB=3,
∴BC=3$\sqrt{3}$,
AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+(3\sqrt{3})^{2}}$=6(米).
(2)在Rt△AFD中,DF=DE-EF=x-3,
∴AF=$\frac{x-3}{tan30°}$=$\sqrt{3}$(x-3),
∵AF=BE=BC+CE,
∴$\sqrt{3}$(x-3)=3$\sqrt{3}$+$\frac{\sqrt{3}}{3}$x,
解得x=9.
答:树高为9米.
点评 本题考查了解直角三角形的应用,解题的关键是正确的构造直角三角形并选择正确的边角关系解直角三角形,难度一般.

练习册系列答案
相关题目
11.“十年树木,百年树人”,教师的素养关系到国家的未来.我区招聘音乐教师采用笔试、专业技能测试、说课三种形式进行选拔,这三项的成绩满分均为100分,并分别按2:3:5的比例折算总分,最后,按照折算后成绩的排序从高到低依次录取.该区要招聘2名音乐教师,而参与的6名选手的各项成绩见下表:
(1)笔试成绩的极差是多少?
(2)写出说课成绩的中位数、众数;
(3)已知序号为1,2,3,4,5号选手的成绩已经折算出,分别为84.2分,84.6分,88.1分,80.8分,86.4分,请计算6号选手的成绩,并判断这六位选手中序号是多少的选手将被录用?为什么?
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 笔试成绩 | 66 | 90 | 86 | 64 | 65 | 84 |
| 专业技能测试成绩 | 95 | 92 | 93 | 80 | 88 | 92 |
| 说课成绩 | 85 | 78 | 86 | 88 | 94 | 85 |
(2)写出说课成绩的中位数、众数;
(3)已知序号为1,2,3,4,5号选手的成绩已经折算出,分别为84.2分,84.6分,88.1分,80.8分,86.4分,请计算6号选手的成绩,并判断这六位选手中序号是多少的选手将被录用?为什么?
 如图所示,一个正方体被截去一个小正方体,则此立体图形的左视图是( )
如图所示,一个正方体被截去一个小正方体,则此立体图形的左视图是( )



 如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(-4,1),点C的坐标为(-1,1),将Rt△ABC按一定的规律变换:第一次,将Rt△ABC沿AC边翻折,得Rt△AB1C;第二次,将Rt△AB1C绕点B1逆时针旋转90°,得Rt△A1B1C1;第三次,将Rt△A1B1C1沿A1C1边翻折,得Rt△A1B2C1;第四次,将Rt△A1B2C1绕点B2逆时针90°,得Rt△A2B2C2…如此依次下去
如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(-4,1),点C的坐标为(-1,1),将Rt△ABC按一定的规律变换:第一次,将Rt△ABC沿AC边翻折,得Rt△AB1C;第二次,将Rt△AB1C绕点B1逆时针旋转90°,得Rt△A1B1C1;第三次,将Rt△A1B1C1沿A1C1边翻折,得Rt△A1B2C1;第四次,将Rt△A1B2C1绕点B2逆时针90°,得Rt△A2B2C2…如此依次下去 若把一组邻边的平方和与一条对角线的平方相等的四边形叫做勾股四边形,则矩形、直角梯形都是勾股四边形.如图,将△ABC绕点B顺时针旋转60°得到△DBE,且∠BCD=30°.
若把一组邻边的平方和与一条对角线的平方相等的四边形叫做勾股四边形,则矩形、直角梯形都是勾股四边形.如图,将△ABC绕点B顺时针旋转60°得到△DBE,且∠BCD=30°. 如图,在?ABCD中,对角线AC与BD相交于点O,BD=2AB,E是OA的中点.求证:BE⊥AC.
如图,在?ABCD中,对角线AC与BD相交于点O,BD=2AB,E是OA的中点.求证:BE⊥AC. 如图,点P是正方形ABCD的对角线BD上的一个动点(不与B、D重合),连结AP,过点B作直线AP的垂线,垂足为H,连结DH.若正方形的边长为4,则线段DH长度的最小值是2$\sqrt{5}$-2.
如图,点P是正方形ABCD的对角线BD上的一个动点(不与B、D重合),连结AP,过点B作直线AP的垂线,垂足为H,连结DH.若正方形的边长为4,则线段DH长度的最小值是2$\sqrt{5}$-2.