Question

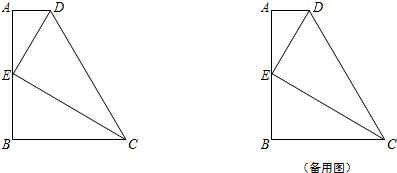
5．已知：如图，在梯形ABCD中，AD∥BC，AB⊥BC，$AB=2\sqrt{3}$．E是边AB的中点，联结DE、CE，且DE⊥CE．设AD=x，BC=y．
（1）如果∠BCD=60°，求CD的长；
（2）求y关于x的函数解析式，并写出自变量x的取值范围；
（3）联结BD．如果△BCD是以边CD为腰的等腰三角形，求x的值．

Answer 1

分析 （1）首先过点D作DH⊥BC，垂足为点H，由AD∥BC，AB⊥BC，DH⊥BC，可求得DH的长，然后设CH=x，则 CD=2x，利用勾股定理即可求得方程：x²+（2$\sqrt{3}$）²=4x²，解此方程即可求得答案；
（2）首先取CD的中点F，连接EF，由梯形的中位线，可表示出EF的长，易得四边形ABHD是平行四边形，然后由勾股定理可得：（y-x）²+12=（x+y）²，继而求得答案；
（3）分别从CD=BD或CD=BC去分析求解即可求得答案．

解答 解：（1）过点D作DH⊥BC，垂足为点H．
∵AD∥BC，AB⊥BC，DH⊥BC，
∴DH=AB=2$\sqrt{3}$，
在Rt△DHC中，
∵∠BCD=60°，
∴∠CDH=30°．
∴CD=2CH，
设CH=x，则 CD=2x．
利用勾股定理，得 CH²+DH²=CD²．
即得：x²+（2$\sqrt{3}$）²=4x²．
解得 x=2（负值舍去）．
∴CD=4；

（2）取CD的中点F，连接EF，
∵E为边AB的中点，
∴EF=$\frac{1}{2}$（AD+BC）=$\frac{1}{2}$（x+y）．
∵DE⊥CE，
∴∠DEC=90°．
又∵DF=CF，
∴CD=2EF=x+y．
由AB⊥BC，DH⊥BC，得∠B=∠DHC=90°．
∴AB∥DH．
又∵AB=DH，
∴四边形ABHD是平行四边形．
∴BH=AD=x．
即得 CH=|y-x|，
在Rt△DHC中，利用勾股定理，得 CH²+DH²=CD²．
即得 （y-x）²+12=（x+y）²．
解得 $y=\frac{3}{x}$，
∴所求函数解析式为$y=\frac{3}{x}$．
自变量x的取值范围是x＞0，且$x≠\sqrt{3}$；

（3）当△BCD是以边CD为腰的等腰三角形时，有两种可能情况：CD=BD或CD=BC．
（ i）如果CD=BD，由DH⊥BC，得 BH=CH．即得 y=2x．
利用 $y=\frac{3}{x}$，得 $2x=\frac{3}{x}$．
解得 $x{_1}=\frac{{\sqrt{6}}}{2}$，$x{_2}=-\frac{{\sqrt{6}}}{2}$．
经检验：$x{_1}=\frac{{\sqrt{6}}}{2}$，$x{_2}=-\frac{{\sqrt{6}}}{2}$，且$x{_2}=-\frac{{\sqrt{6}}}{2}$不合题意，舍去．
∴$x=\frac{{\sqrt{6}}}{2}$；
（ ii）如果CD=BC，则 x+y=y．
即得 x=0（不合题意，舍去），
综上可得：$x=\frac{{\sqrt{6}}}{2}$．

点评 此题属于四边形的综合题．考查了梯形的性质、平行四边形的判定与性质、等腰三角形的性质以及勾股定理等知识．注意掌握辅助线的作法，掌握方程思想与分类讨论思想的应用是解此题的关键．