题目内容
12. 如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.(1)△ABC的面积为8;
(2)画出△ABC的中线AE;
(3)将△ABC经过平移后得到△A′B′C′,图中标出了点B的对应点B′,补全△A′B′C′;
(4)连接AA′,BB′,则这两条线段之间的关系是平行且相等;
(5)能使S△ABC=S△QBC的格点Q共有4个(A点除外).
分析 (1)利用三角形的面积公式:底×高×$\frac{1}{2}$进行计算即可;
(2)找出BC的中点E,连接AE即可;
(3)点B向左平移到2个单位,向上平移4个单位平移到B′位置,点A、C也向左平移到2个单位,向上平移4个单位平移到对应点位置,再连接即可;
(4)根据平移的性质:图形平移后,对应线段平行且相等可得答案;
(5)过A作BC的平行线,点Q在此平行线上.
解答 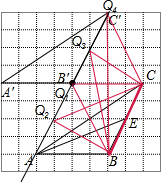 解:(1)△ABC的面积为:$\frac{1}{2}$×4×4=8,
解:(1)△ABC的面积为:$\frac{1}{2}$×4×4=8,
故答案为:8;
(2)如图所示;
(3)如图所示;
(4)AA′与BB′平行且相等,
故答案为:平行且相等;
(5)如图所示:格点Q共有4个.
故答案为:4.
点评 此题主要考查了作图--平移变换,以及平移的性质、三角形的面积,关键是正确确定A、B、C三点平移后的位置.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
7.若一个正数的平方根是2a-1和-a+2,则这个正数是( )
| A. | 1 | B. | 3 | C. | 4 | D. | 9 |
8.下列关于向量的等式中,正确的是( )
| A. | $\overrightarrow{AB}+\overrightarrow{BA}=0$ | B. | $\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{BC}$ | C. | $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{CB}$ | D. | $\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}=\overrightarrow 0$ |
17. 如图所示,该几何体的主视图是( )
如图所示,该几何体的主视图是( )
 如图所示,该几何体的主视图是( )
如图所示,该几何体的主视图是( )| A. |  | B. |  | C. |  | D. |  |
4.如图,已知某几何体的三视图(单位:cm),则该几何体的侧面积等于( )


| A. | 12πcm2 | B. | 15πcm2 | C. | 24πcm2 | D. | 30πcm2 |
 如图,已知∠AOB,按下列语句画图:
如图,已知∠AOB,按下列语句画图: