题目内容
2. 如图,菱形ABCD的周长为8cm,高AE长为$\sqrt{3}$cm,求对角线BD的长.
如图,菱形ABCD的周长为8cm,高AE长为$\sqrt{3}$cm,求对角线BD的长.
分析 先根据周长和菱形的四边相等求边长为2cm,由勾股定理求BE的长,从而求CE的长;根据等腰三角形三线合一得AC=AB,最后利用菱形面积的两种求法列等式求出对角线BD的长.
解答 解:∵菱形ABCD的周长为8cm,
∴AB=BC=2,
由勾股定理得:BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=$\sqrt{{2}^{2}-(\sqrt{3})^{2}}$=1,
∴CE=BC-BE=2-1=1,
∴CE=BE,
∵AE⊥BC,
∴AC=AB=2,
∴S菱形ABCD=BC•AE=$\frac{1}{2}$AC•BD,
∴2×$\sqrt{3}$=$\frac{1}{2}$×2BD,
∴BD=2$\sqrt{3}$,
答:对角线BD的长为2$\sqrt{3}$cm.
点评 本题考查了菱形的性质,熟练掌握菱形的性质是做好本题的关键;同时运用勾股定理求边长;对于菱形的面积公式的两种计算方法,既可以求面积,也可以利用此等量关系列式求边长.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
17.一次劳技课上,老师让同学们在一张长为8cm,宽为6cm的长方形纸片上,剪下一个腰长为5cm的等腰三角形,要求等腰三角形的一个顶点与长方形的一个顶点重合,其余的两个顶点在长方形的边上,则剪下的等腰三角形的面积不可能为( )
| A. | 10cm2 | B. | 5$\sqrt{6}$cm2 | C. | 7$\sqrt{3}$cm2 | D. | $\frac{25}{2}$cm2 |
7.三条边都是质数的三角形可能是( )
①锐角三角形②直角三角形③钝角三角形④等腰三角形⑤等边三角形.
①锐角三角形②直角三角形③钝角三角形④等腰三角形⑤等边三角形.
| A. | ①②③④ | B. | ②③④⑤ | C. | ①③④⑤ | D. | ①②③④⑤ |
 如图,△ABC中,AB=AC,∠BAC=120°,AD⊥AC交BC于点D,BD=1,求BC的长.
如图,△ABC中,AB=AC,∠BAC=120°,AD⊥AC交BC于点D,BD=1,求BC的长. 如图,A(0,$\sqrt{3}$),B(-1,0),C为x轴上一点,四边形为菱形
如图,A(0,$\sqrt{3}$),B(-1,0),C为x轴上一点,四边形为菱形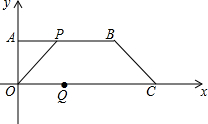 在平面直角坐标系中,有点A(0,4)、B(9,4),C(12,0).已知点P从点A出发沿AB路线向点B运动,点Q从点C出发沿CO路线向点O运动.运动速度都是每秒一个单位长度,运动时间为t秒.
在平面直角坐标系中,有点A(0,4)、B(9,4),C(12,0).已知点P从点A出发沿AB路线向点B运动,点Q从点C出发沿CO路线向点O运动.运动速度都是每秒一个单位长度,运动时间为t秒. 如图,平行四边形ABCD中,E是BC边上的点,AE交BD于点F,如果$\frac{BE}{EC}$=2,求$\frac{{S}_{△BFE}}{{S}_{△DFA}}$.
如图,平行四边形ABCD中,E是BC边上的点,AE交BD于点F,如果$\frac{BE}{EC}$=2,求$\frac{{S}_{△BFE}}{{S}_{△DFA}}$.