题目内容
6．
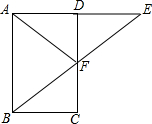如图，矩形ABCD中，点E在线段AD延长线上，AD=DE，连接BE与DC相交于点F，连接AF，请从图中找出一个等腰三角形△AFE（答案不唯一）．
分析 由矩形的性质得出DF⊥AE，由线段垂直平分线的性质得出AF=EF即可．
解答 解：△AFE是等腰三角形；理由如下：
∵四边形ABCD是矩形，
∴∠ADF=90°，
即DF⊥AE，
又∵AD=DE，
∴AF=EF，即△AFE是等腰三角形．
故答案为：△AFE（答案不唯一）．
点评 本题考查了矩形的性质、线段垂直平分线的性质；熟练掌握矩形的性质，由线段垂直平分线的性质得出AF=EF是解决问题的关键．
练习册系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
16．一个均匀的小立方体，它的6个面上分别标有实数5.1，$\frac{3}{4}$，$\sqrt{16}$，$\frac{π}{2}$，$\sqrt{11}$，8.$\stackrel{•}{2}0\stackrel{•}{3}$，任意掷出这个小立方体，朝上的面标有无理数的概率是（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
17．近年来，中国高铁发展迅速，高铁技术不断走出国门，成为展示我国实力的新名片．预计到2015年底，中国高速铁路营运里程将达到18000公里．将18000用科学记数法表示应为（ ）
| A． | 18×103 | B． | 1.8×103 | C． | 1.8×104 | D． | 1.8×105 |
如图所示的坐标系中，△ABC的三个顶点的坐标依次为A（-1，2），B（-4，1），C（-2，-2）．
如图，正方形ABCD的对角线AC与BD相交于点O，∠ACB的角平分线分别交AB、BD于M、N两点，若AM=2，则线段ON的长为1．