题目内容
4. 如图,四边形ABCD的两条对角线AC,BD互相垂直,AC+BD=10,当AC,BD的长是多少时,四边形ABCD的面积最大?
如图,四边形ABCD的两条对角线AC,BD互相垂直,AC+BD=10,当AC,BD的长是多少时,四边形ABCD的面积最大?
分析 直接利用对角线互相垂直的四边形面积求法得出S=$\frac{1}{2}$AC•BD,再利用配方法求出二次函数最值.
解答 解:设AC=x,四边形ABCD面积为S,则BD=10-x,
则:S=$\frac{1}{2}$AC•BD=$\frac{1}{2}$x(10-x)=-$\frac{1}{2}$(x-5)2+$\frac{25}{2}$,
当x=5时,S最大=$\frac{25}{2}$;所以AC=BD=5时,四边形ABCD的面积最大.
点评 此题主要考查了二次函数最值以及四边形面积求法,正确掌握对角线互相垂直的四边形面积求法是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.已知二次函数y=a(x-1)2+c(a>0),当自变量x分别取-$\sqrt{3}$、0、3时,对应的函数值分别为:y1,y2,y3,则y1,y2,y3的大小关系正确的是( )
| A. | y3<y2<y1 | B. | y1<y2<y3 | C. | y3<y1<y2 | D. | y2<y3<y1 |
12.如果|a|=3,|b|=2,且a-b<0.那么a+b的值是( )
| A. | -1,-5 | B. | 1,5 | C. | ±5 | D. | ±1 |
9.方程4x2-8x-25=0的一次项系数和常数项分别为( )
| A. | -2,25 | B. | -2,-25 | C. | 8,-25 | D. | -8,-25 |
16.下列关于有理数加减法表示正确的是( )
| A. | a>0 b<0,并且|a|>|b|,则a+b=|a|+|b| | B. | a<0 b>0,并且|a|>|b|,则a+b=|a|-|b| | ||
| C. | a<0 b>0,并且|a|<|b|,则a-b=|b|+|a| | D. | a<0 b<0,并且|a|>|b|,则a-b=|b|-|a| |
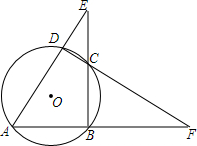 如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F.
如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F. 如图,抛物线y=$\frac{1}{4}$x2-$\frac{5}{4}$x+1与x轴的正半轴相交于点A,B(点A位于点B的左侧),与y轴的正半轴交于点.
如图,抛物线y=$\frac{1}{4}$x2-$\frac{5}{4}$x+1与x轴的正半轴相交于点A,B(点A位于点B的左侧),与y轴的正半轴交于点.