题目内容
14.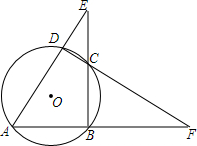 如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F.
如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F.(1)当∠E=∠F时,则∠ADC=90°;
(2)当∠A=55°,∠E=30°时,求∠F的度数;
(3)若∠E=α,∠F=β,且α≠β.请你用含有α、β的代数式表示∠A的大小.
分析 (1)由∠E=∠F,易得∠ADC=∠ABC,又由圆的内接四边形的性质,即可求得答案;
(2)由∠A=55°,∠E=30°,首先可求得∠ABC的度数,继而利用圆的内接四边形的性质,求得∠ADC的度数,则可求得答案;
(3)由三角形的内角和定理与圆的内接四边形的性质,即可求得180°-∠A-∠F+180°-∠A-∠E=180°,继而求得答案.
解答 解:(1)∵∠E=∠F,∠DCE=∠BCF,∠ADC=∠E+∠DCE,∠ABC=∠BCF+∠F,
∴∠ADC=∠ABC,
∵四边形ABCD是⊙O的内接四边形,
∴∠ADC+∠ABC=180°,
∴∠ADC=90°.
故答案为:90°;
(2)∵在△ABE中,∠A=55°,∠E=30°,
∴∠ABE=180°-∠A-∠E=95°,
∴∠ADF=180°-∠ABE=85°,
∴在△ADF中,∠F=180°-∠ADF-∠A=40°;
(3)∵∠ADC=180°-∠A-∠F,∠ABC=180°-∠A-∠E,
∵∠ADC+∠ABC=180°,
∴180°-∠A-∠F+180°-∠A-∠E=180°,
∴2∠A+∠E+∠F=180°,
∴∠A=90°-$\frac{∠E+∠F}{2}$=90°-$\frac{α+β}{2}$.
点评 此题考查了圆的内接四边形的性质以及圆的内接四边形的性质.注意圆内接四边形的对角互补.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.圆、平行四边形、等腰三角形、菱形,矩形的卡片任意摆放,将有图形的一面朝下,从中任意翻开一张,如果翻开的图形是轴对称图形,就可以过关.那么一次过关的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
5.下列四个图案中,不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
9.若关于x的方程ax2+2x-1=0无解,则a的值可以是( )
| A. | 1 | B. | 0 | C. | -1 | D. | -2 |
 若实数a、b、c在数轴上的位置如图所示,且|a|=|b|,化简|a|+|a+b|-$\sqrt{{{(c-a)}^2}}$一2$\sqrt{c^2}$.
若实数a、b、c在数轴上的位置如图所示,且|a|=|b|,化简|a|+|a+b|-$\sqrt{{{(c-a)}^2}}$一2$\sqrt{c^2}$. 如图,四边形ABCD的两条对角线AC,BD互相垂直,AC+BD=10,当AC,BD的长是多少时,四边形ABCD的面积最大?
如图,四边形ABCD的两条对角线AC,BD互相垂直,AC+BD=10,当AC,BD的长是多少时,四边形ABCD的面积最大?