题目内容
19．已知：△ABC中，AB=AC，BD是AC上的高，且∠CBD=35°，则∠A=70°．分析 根据高的定义和直角三角形的性质得到∠C=55°，再根据等腰三角形的性质和三角形内角和定理可得∠A的度数．
解答 解：∵BD是AC上的高，∠CBD=35°，
∴∠C=90°-35°=55°，
∵AB=AC，
∴∠B=∠C=55°，
∴∠A=180°-55°×2=70°．
故答案为：70°．
点评 考查了等腰三角形的性质，关键是得到∠B=55°，以及等腰三角形的两个底角相等．
练习册系列答案
相关题目
9．若关于x的方程ax2+2x-1=0无解，则a的值可以是（ ）
| A． | 1 | B． | 0 | C． | -1 | D． | -2 |
10．在3.14、-$\sqrt{2}$、$\root{3}{27}$、π、0.2020020002…这六个数中，无理数有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
如图，四边形ABCD的两条对角线AC，BD互相垂直，AC+BD=10，当AC，BD的长是多少时，四边形ABCD的面积最大？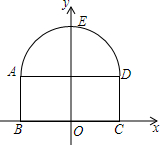
如图，隧道的截面由抛物线AED和矩形ABCD构成，矩形的长BC为8m，宽AB为2m，以BC所在的直线为x轴，线段BC的垂直平分线为y轴，建立平面直角坐标系，y轴是抛物线的对称轴，顶点E到坐标原点O的距离为6m．